x<-seq(-6,6,length=40); y<-x
# Función Normal Bivariada
f<-function(x,y,mu=c(0,0),s=c(1,0,1))
{
mu1<-mu[1]; mu2<-mu[2]
s11<-s[1]; s12<-s[2]; s22<-s[3]; rho<-s12/(s11*s22)
term1<-1/(2*pi*sqrt(s11*s22*(1-rho^2)))
term2<--1/(2*(1-rho^2))
term3<-(x-mu1)^2/s11
term4<-(y-mu2)^2/s22
term5<--2*rho*((x-mu1)*(y-mu2))/(sqrt(s11)*sqrt(s22))
term1*exp(term2*(term3+term4-term5))
}
z<-outer(x,y,f,s=c(5,12.5,5)) # matriz de densidades
persp(x, y, z, col="lightsalmon", theta=30, phi=20, r=50, d=0.1, expand=0.5, ltheta=90,
main="Distribuci?n Normal Bivariada", lphi=180, shade=0.3, ticktype="detailed",
nticks=5, cex.axis=0.7, zlab='Densidad')
mtext(expression(list(mu[x]==0, mu[y]==0, sigma[x]==5, sigma[y]==5,
sigma[xy]==12.5, rho==0.5)), side=3)2 Repaso y Simulación Serie
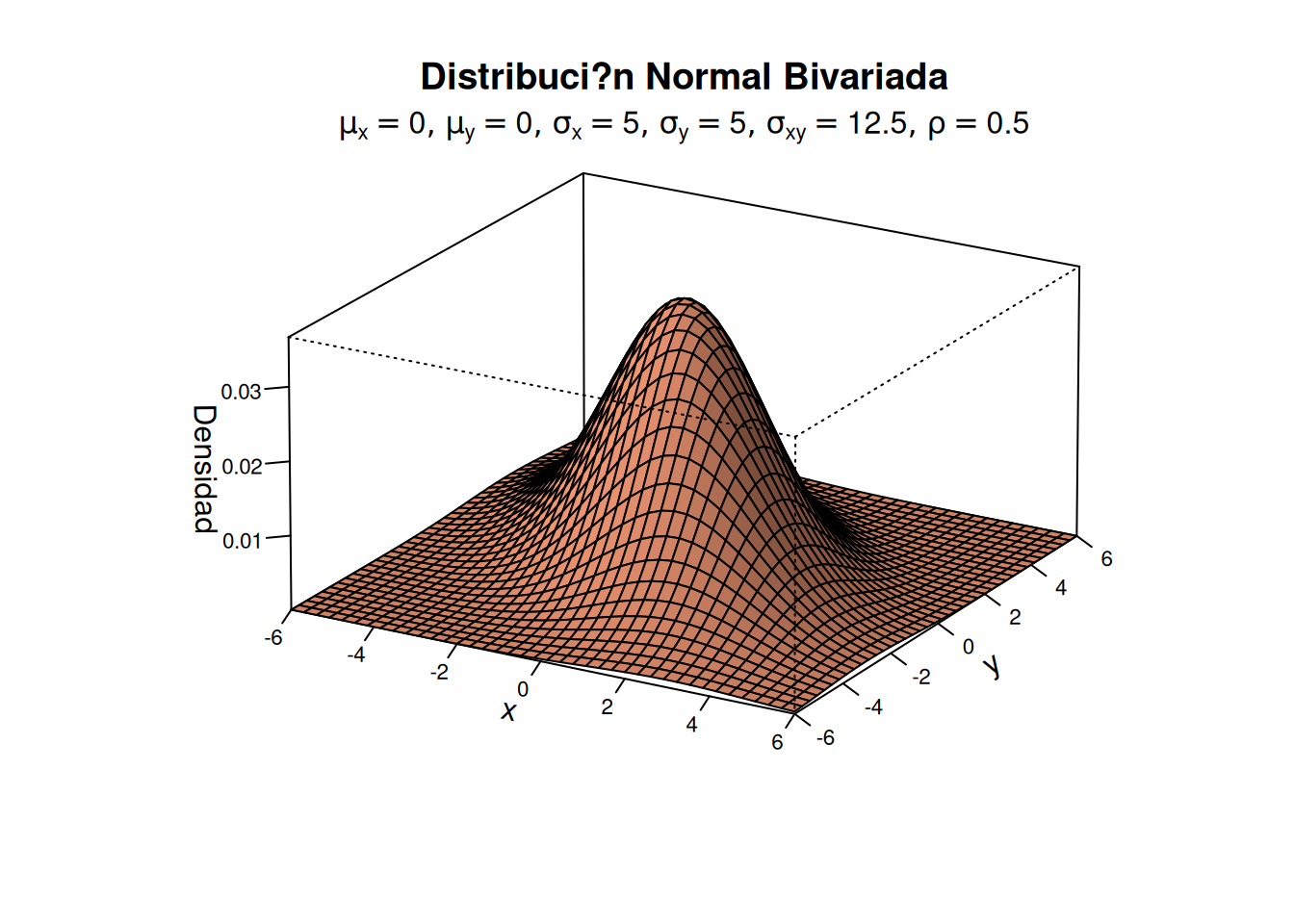
3 DISTRIBUCIÓN NORMAL BIVARIADA
Esta sección limpia el entorno, define la secuencia para x e y, define la función de la distribución normal bivariada y genera el gráfico 3D de la densidad.
4 DISTRIBUCIÓN NORMAL UNIVARIADA 1
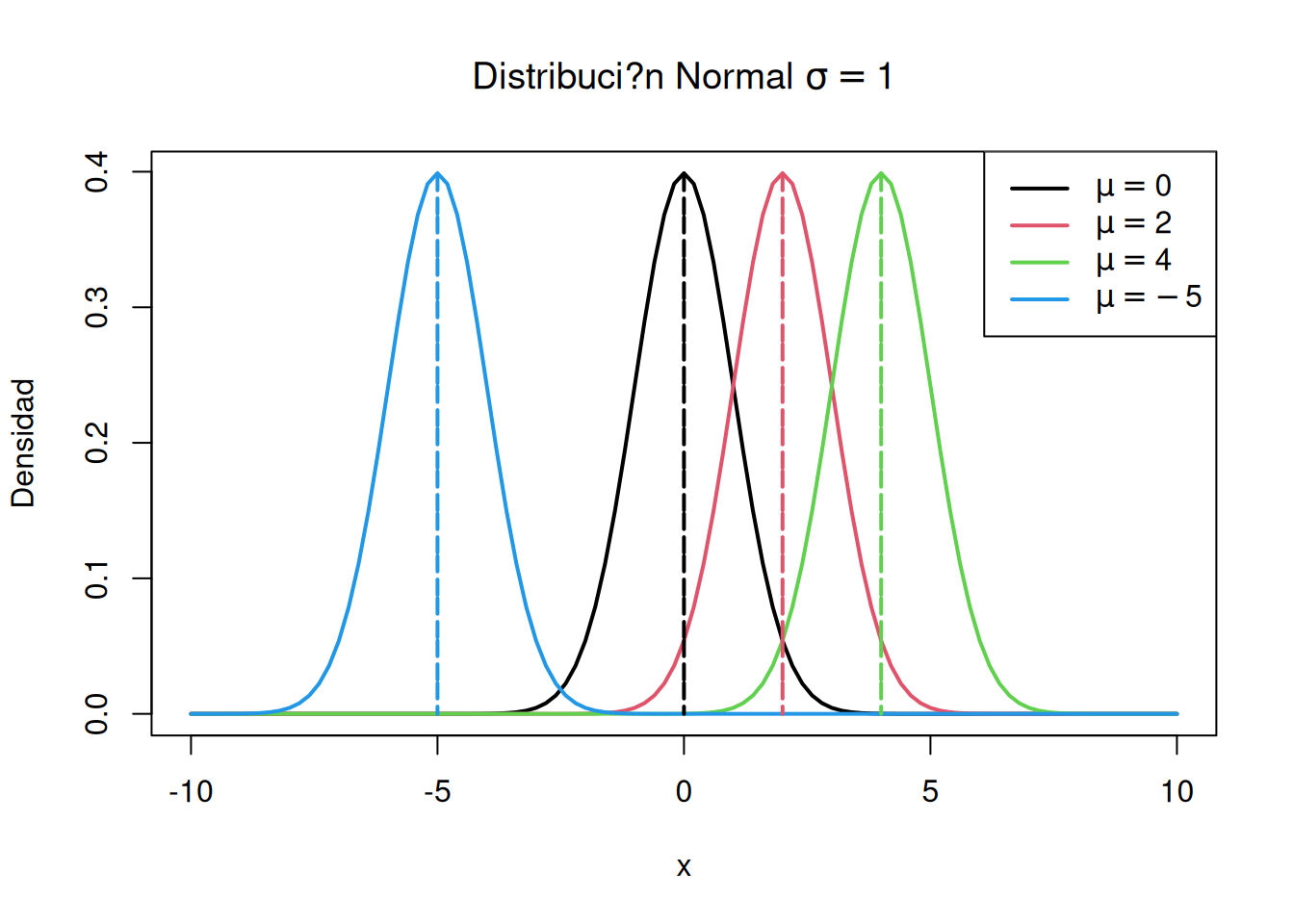
Se explora la normal univariada variando la media y la varianza.
# Variando la media de la distribución
par(mfrow=c(1,1))
mu<-c(0,2,4,-5);
curve(dnorm(x), xlim=c(-10,10), main=expression('Distribuci?n Normal '*sigma==1), lwd=2,
ylab='Densidad')
curve(dnorm(x,2,1), col=2, lwd=2, add=T)
curve(dnorm(x,4,1), col=3, lwd=2, add=T)
curve(dnorm(x,-5,1), col=4, lwd=2, add=T)
for(i in 1:4){ polygon(c(mu[i], mu[i]), c(0, dnorm(mu[i], mu[i], 1)), border=i, lty=4, lwd=2) }
legend('toprigh', lty=1, col=1:4, lwd=2, legend=c(expression(mu==0), expression(mu==2),
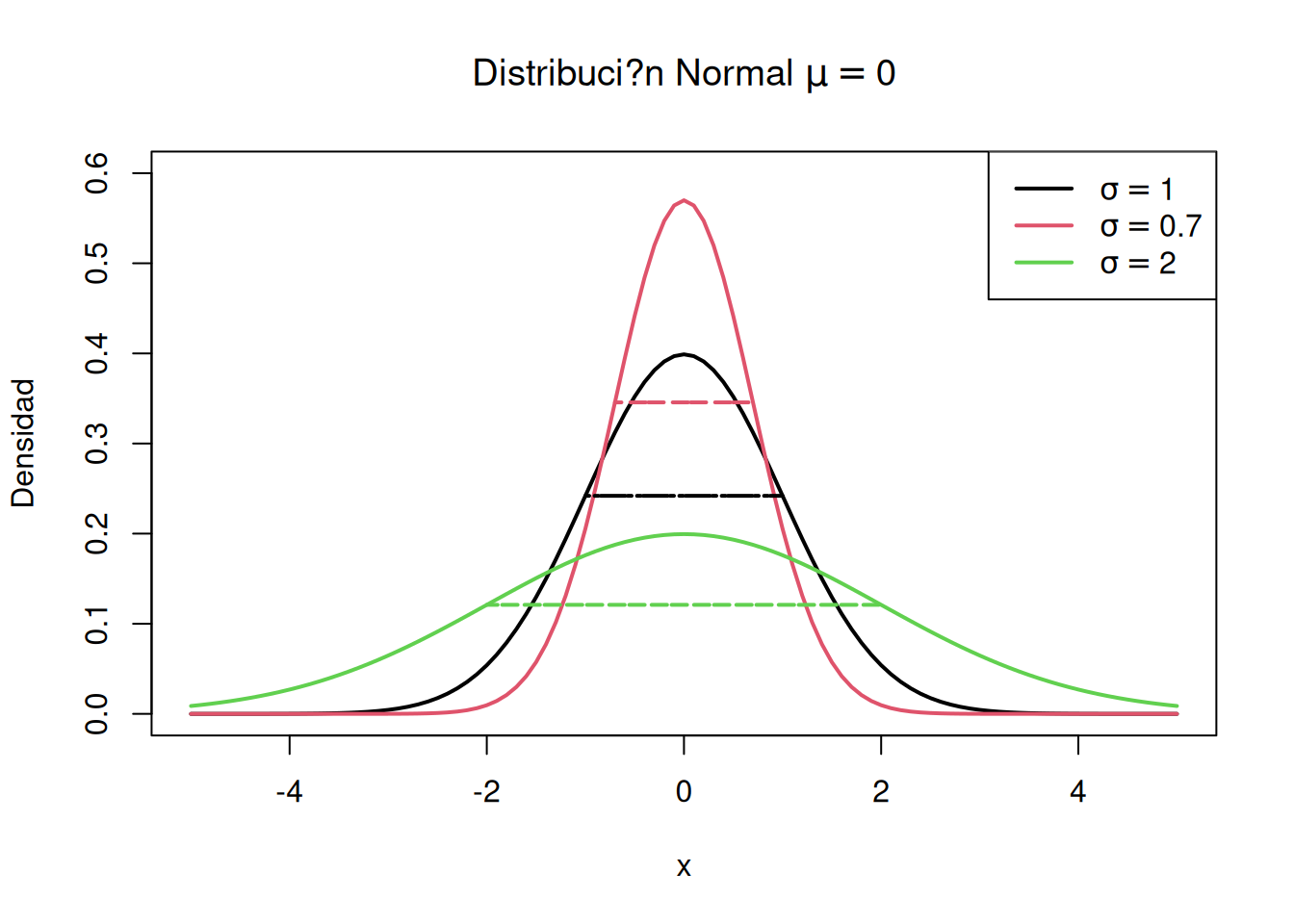
expression(mu==4), expression(mu==-5)))# Variando la varianza de la distribución
sig<-c(1,0.7,2); sig<-cbind(-sig,sig)
curve(dnorm(x), lwd=2, ylim=c(0,0.6), xlim=c(-5,5), ylab='Densidad',
main=expression('Distribuci?n Normal '*mu==0))
curve(dnorm(x,0,sig[2,2]), col=2, lwd=2, add=T)
curve(dnorm(x,0,sig[3,2]), col=3, lwd=2, add=T)
for(i in 1:3){ polygon(sig[i,], dnorm(sig[i,],0,sig[i,2]), border=i, lty=4, lwd=2) }
legend('toprigh', lty=1, col=1:3, lwd=2, legend=c(expression(sigma==1), expression(sigma==0.7),
expression(sigma==2)))library(moments)
kurtosis(dnorm(x))[1] 3.492781kurtosis(dnorm(x,0,sig[2,2]))[1] 5.464751kurtosis(dnorm(x,0,sig[3,2]))[1] 1.6531455 DISTRIBUCIÓN NORMAL UNIVARIADA 2
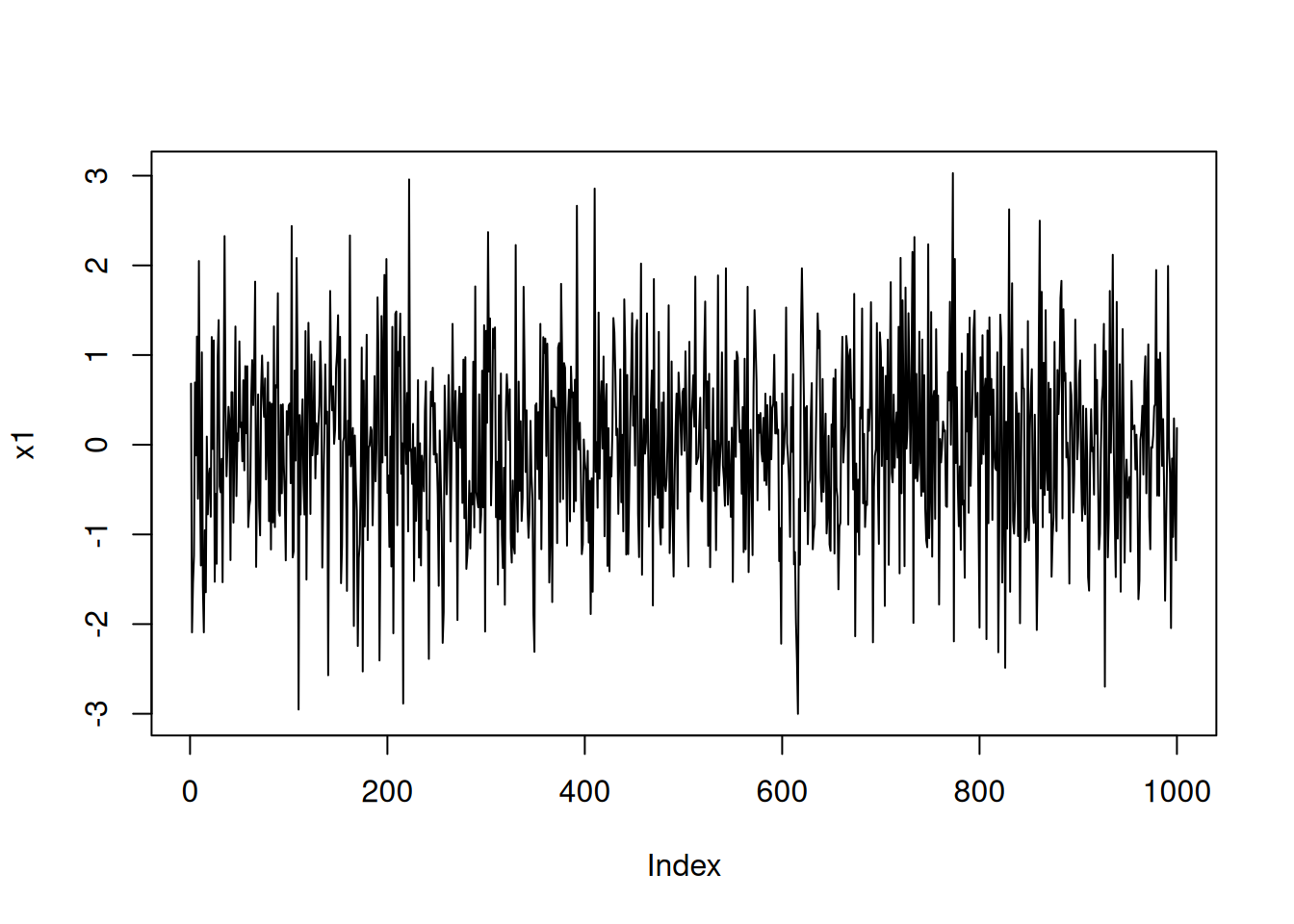
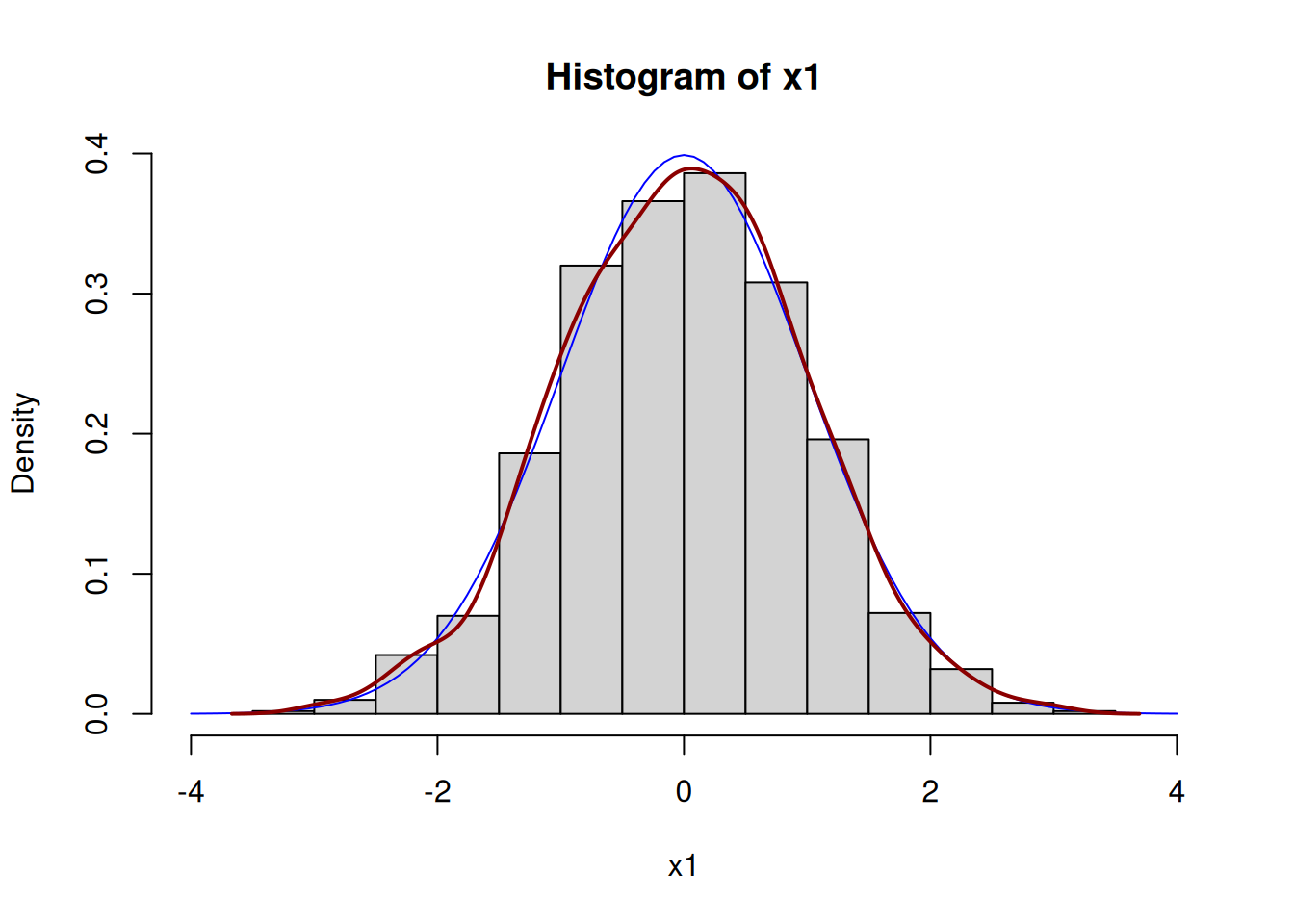
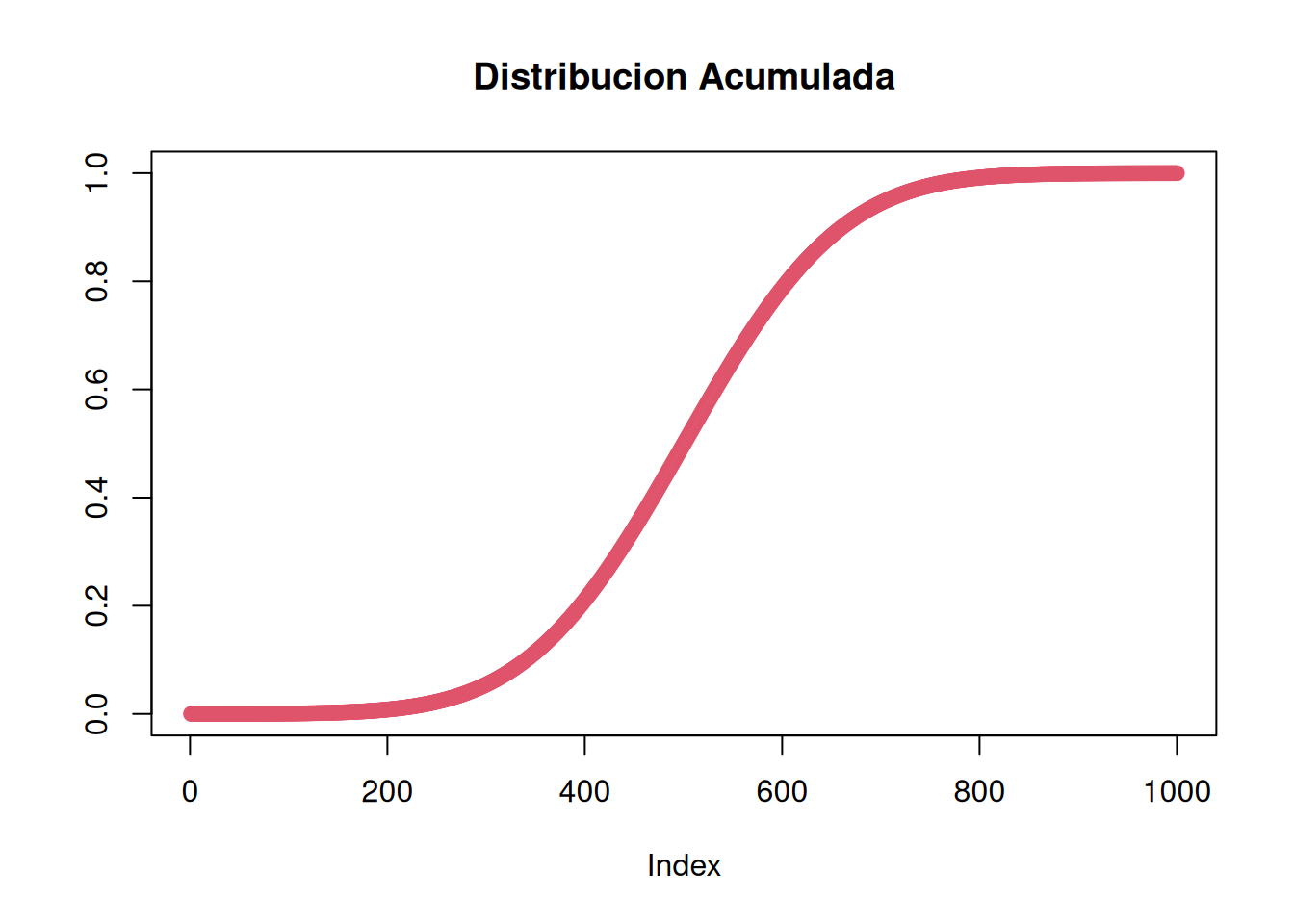
En esta sección se simulan datos normales, se trazan la serie, el histograma, la curva teórica y la estimación de densidad, además de visualizar la distribución acumulada y calcular algunos momentos.
x1<- rnorm(1000, mean=0, sd=1)
par(mfrow=c(1,1))
plot(x1, type="l")hist(x1, freq=FALSE, xlim=c(-4, 4))
curve(dnorm(x), add=T, col="blue")
lines(density(x1), lwd=2, col="darkred")plot(pnorm(seq(-4,4, length.out=1000)), col=2, ylab="", main="Distribucion Acumulada")# Momentos de una variable:
library(moments)
media <- mean(x1)
varianza <- var(x1)
sesgo <- skewness(x1)
curtosis <- kurtosis(x1)
media [1] -0.003691114varianza [1] 0.9672554sesgo [1] -0.02897471curtosis[1] 2.9821616 IMPORTAR BASE DE DATOS Y CREAR SERIE DE TIEMPO
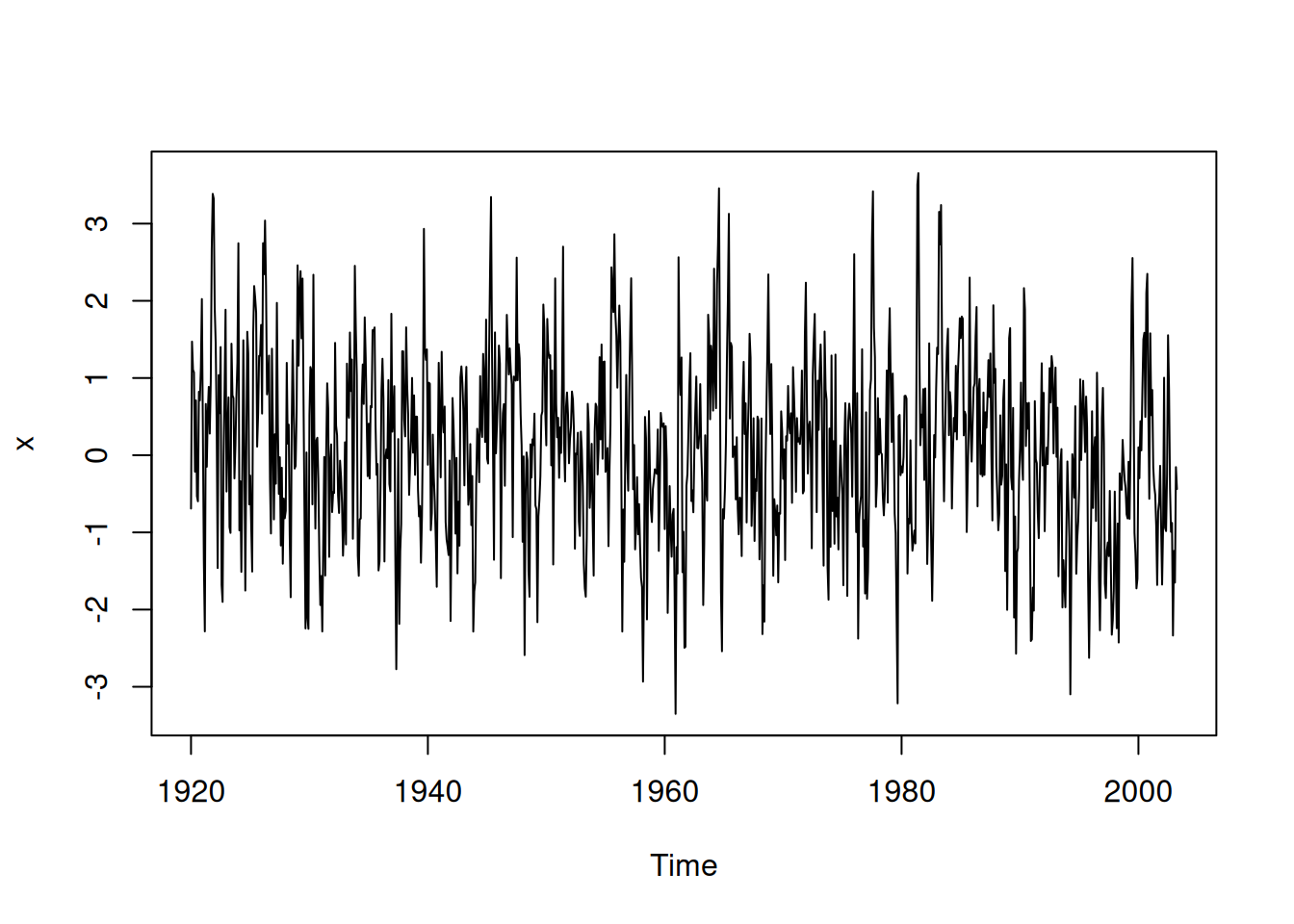
Se muestra cómo importar una base de datos y definir un objeto de serie de tiempo.
#setwd("C:/Users/cubid/Desktop/QUARTO - MATERIAS UNAL/9 SERIES DE TIEMPO/Lesson01")
datos <- read.table("P0_datos.txt", header=T, dec=".", sep="\t")
library(readxl)
datos <- read_excel("P0_datos.xlsx", sheet="datos1") ### Este archivo debe actualizarse cada mes
# definir un objeto de serie de tiempo:
xt <- datos[,2]
xt <- ts(xt, start=c(1920,1), frequency=12)
class(xt)[1] "ts"plot(xt)7 EJEMPLOS DE SERIES DE TIEMPO
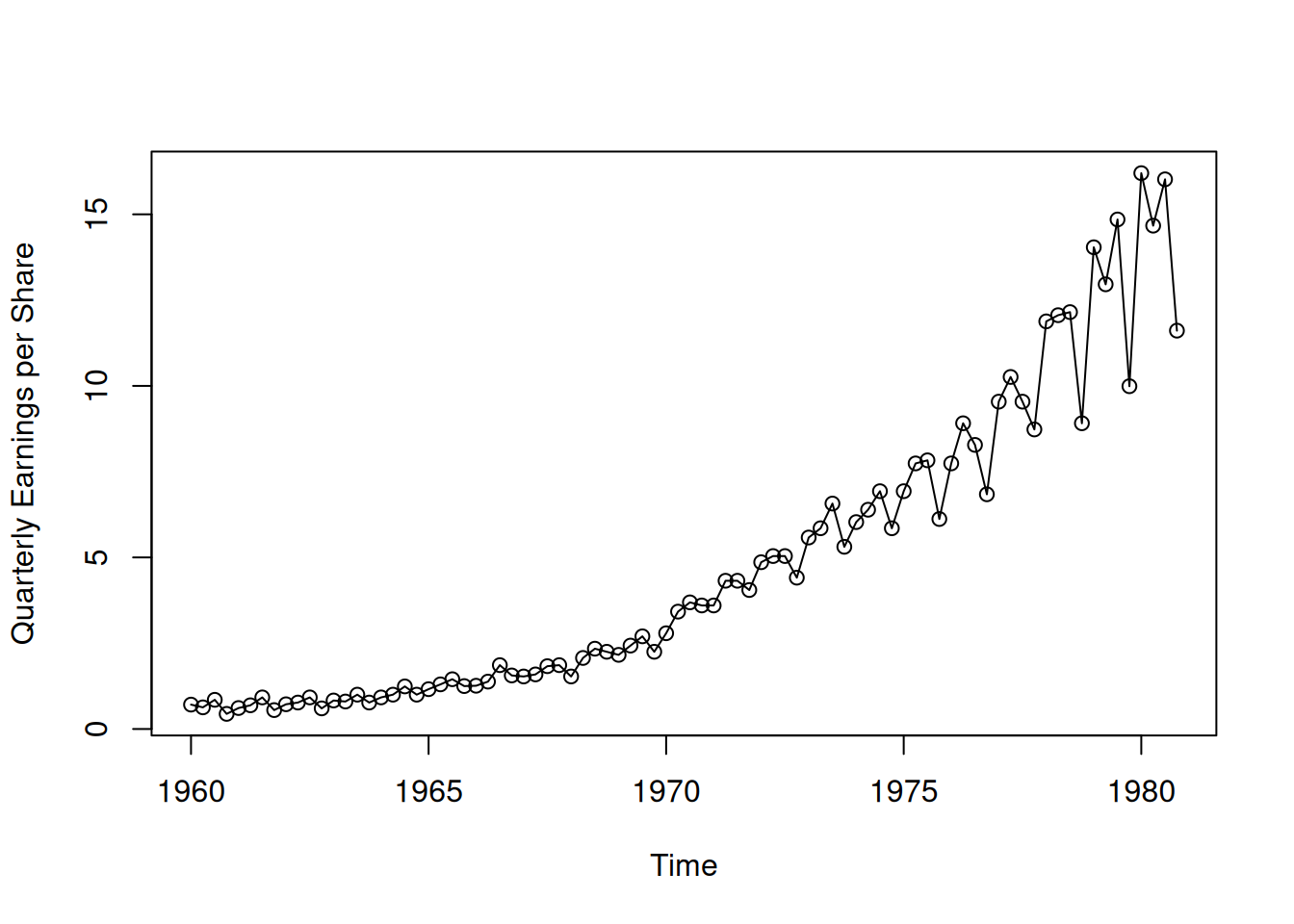
Se presentan diversos ejemplos utilizando datos de series de tiempo.
library(astsa) # Análisis de Series de Tiempo Aplicado
# Ganancias trimestrales de Johnson & Johnson
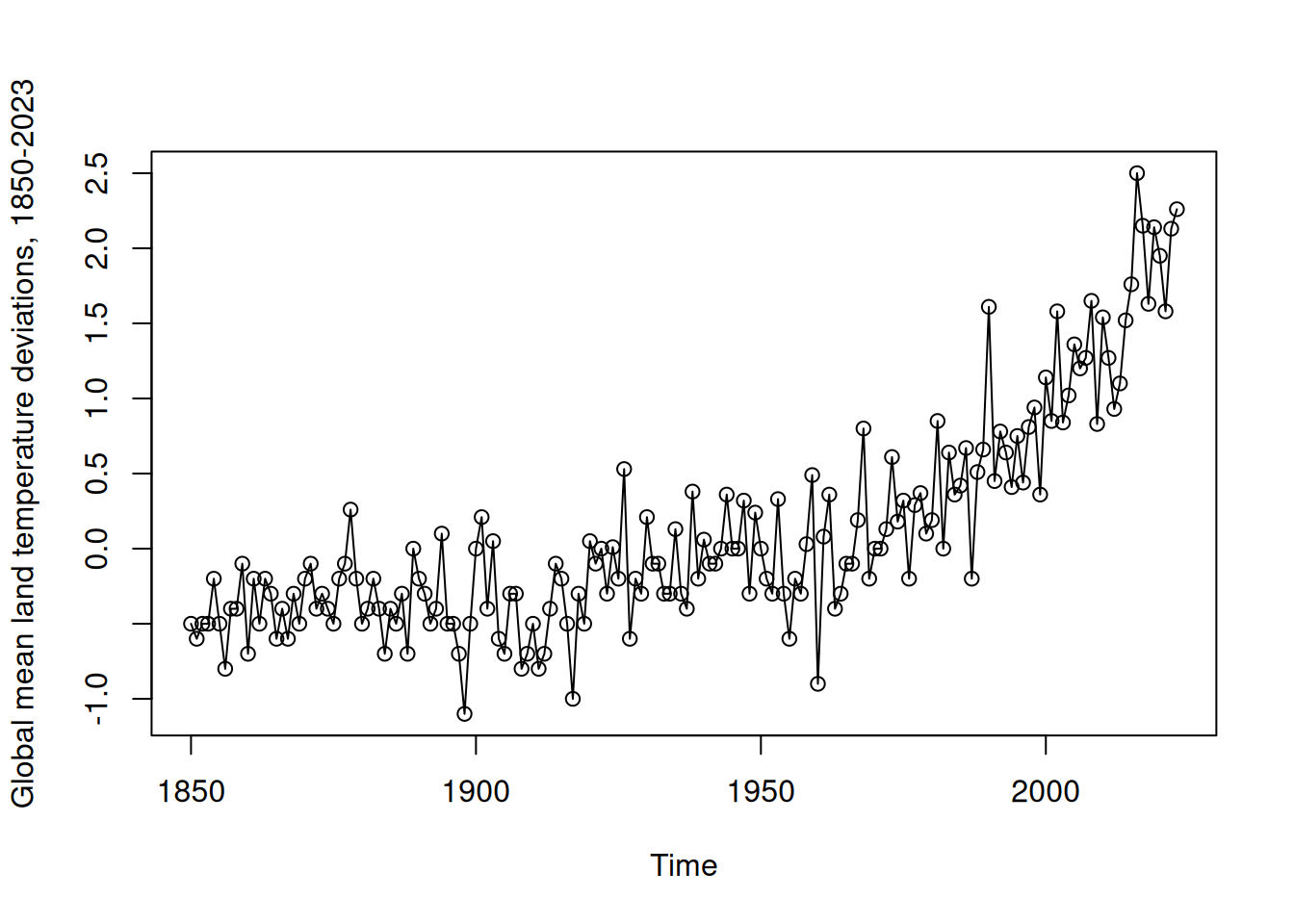
plot(jj, type="o", ylab="Quarterly Earnings per Share")# Calentamiento Global
plot(gtemp_land, type="o", ylab="Global mean land temperature deviations, 1850-2023")# Promedio Industrial Dow Jones
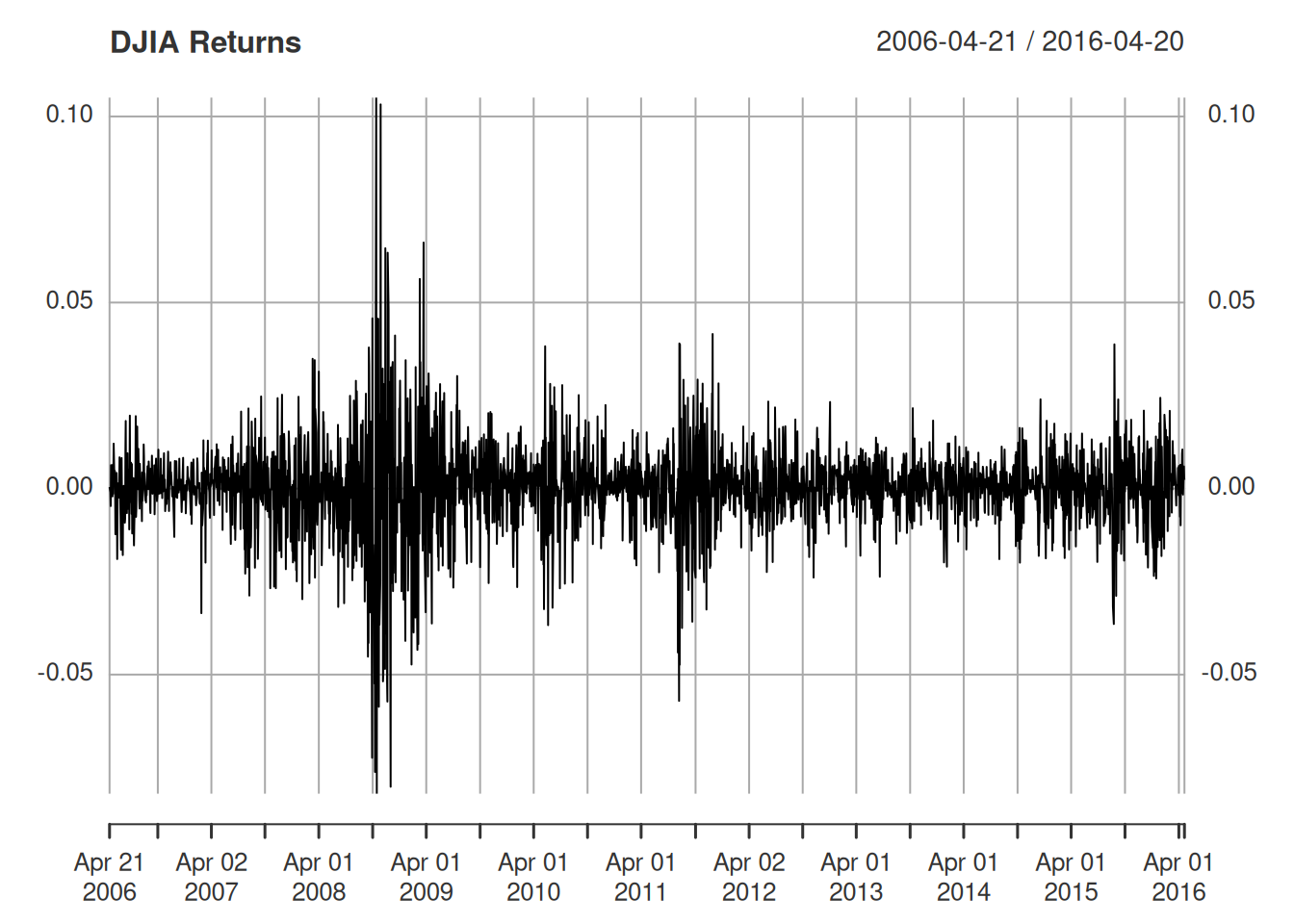
# retornos diarios (o cambio porcentual) del Dow Jones Industrial Average (DJIA)
# desde el 20 de abril, 2006 hasta el 20 de abril, 2016
library(xts)Loading required package: zoo
Attaching package: 'zoo'The following objects are masked from 'package:base':
as.Date, as.Date.numericdjiar = diff(log(djia$Close))[-1] # retornos aproximados
# diff toma el dato t sobre el t-1, le resta 1, y eso define el retorno en t
plot(djiar, main="DJIA Returns", type="n")lines(djiar)# Valores mensuales de una serie ambiental denominada Índice de Oscilación del Sur (SOI)
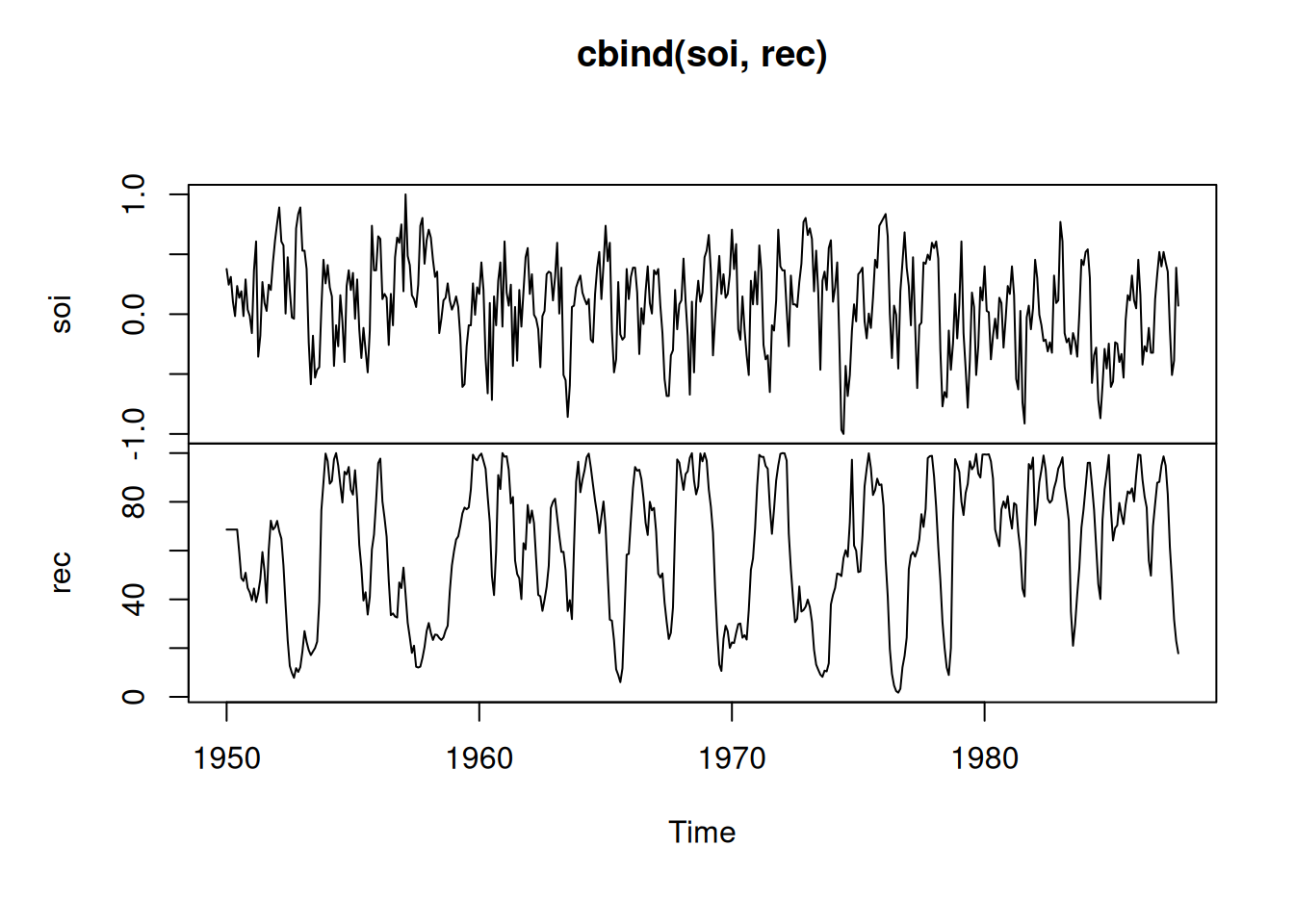
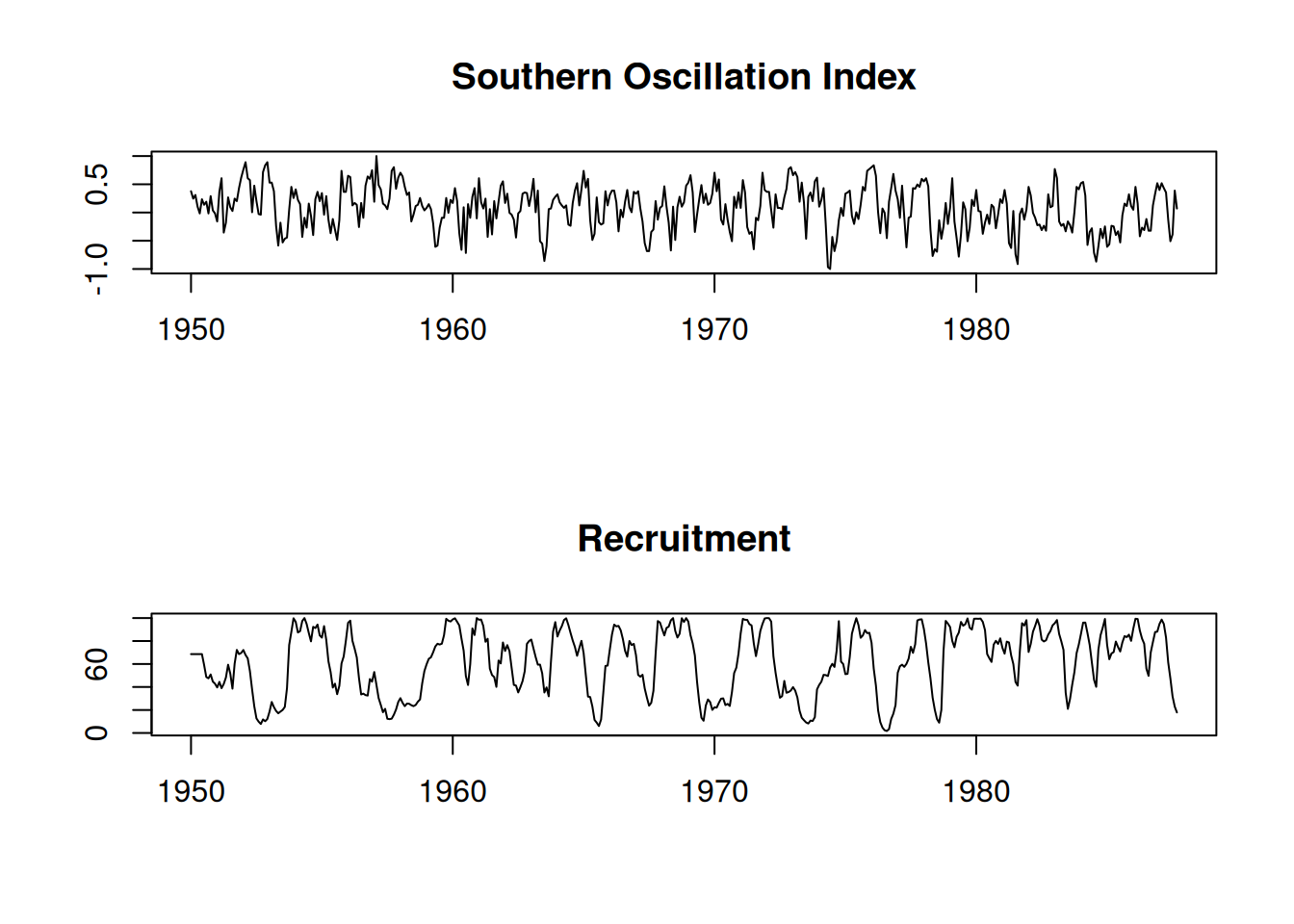
# y Reclutamiento (número de peces nuevos) proporcionados por el Dr. Roy Mendelssohn
# del Grupo de Pesquerías Ambientales del Pacífico.
# Ambas series corresponden a un periodo de 453 meses (1950–1987)
# El SOI mide cambios en la presión atmosférica, relacionados con las temperaturas de la superficie del mar en el Pacífico Central.
plot.ts(cbind(soi, rec))par(mfrow=c(2,1))
plot(soi, ylab='', xlab='', main='Southern Oscillation Index')
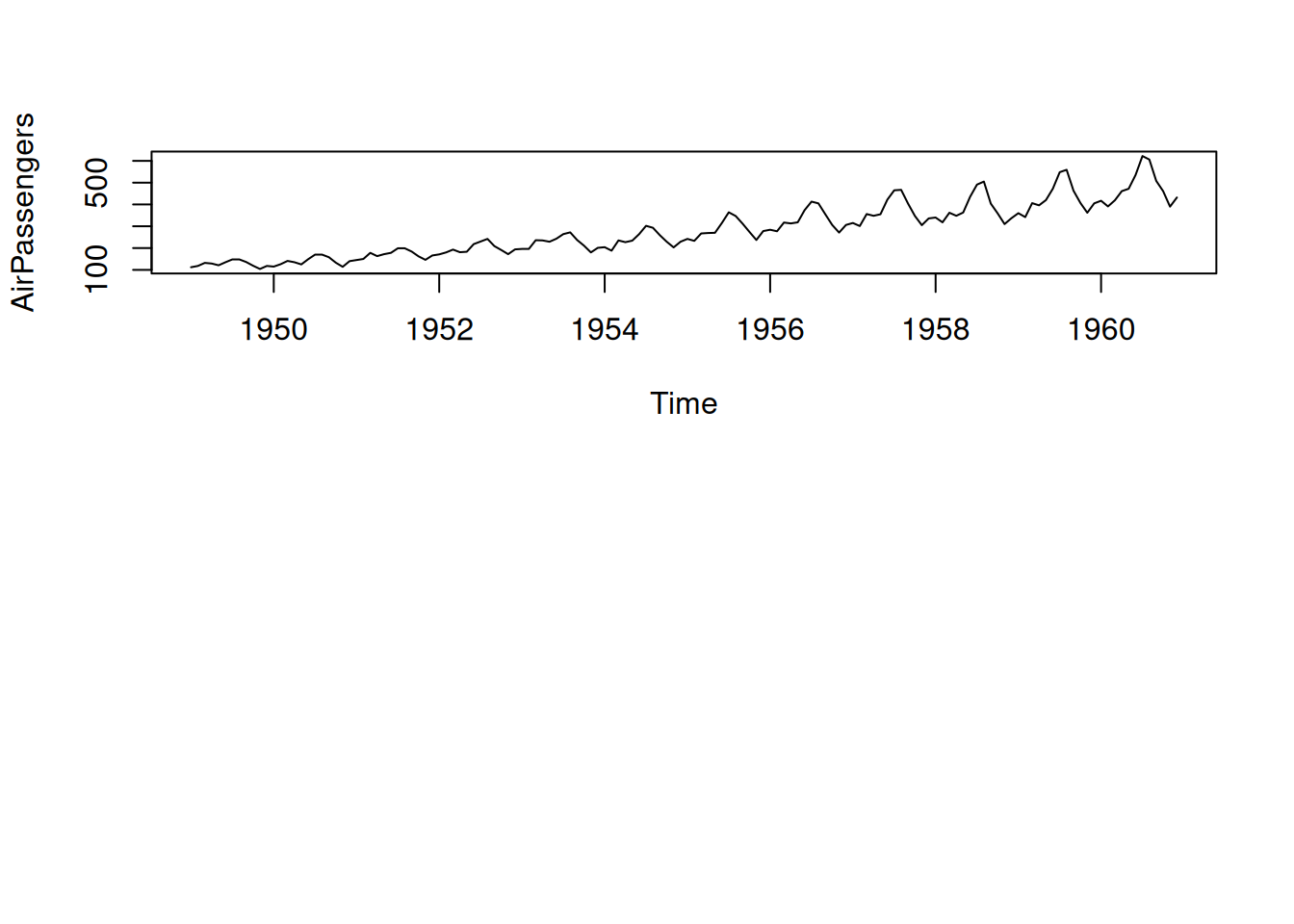
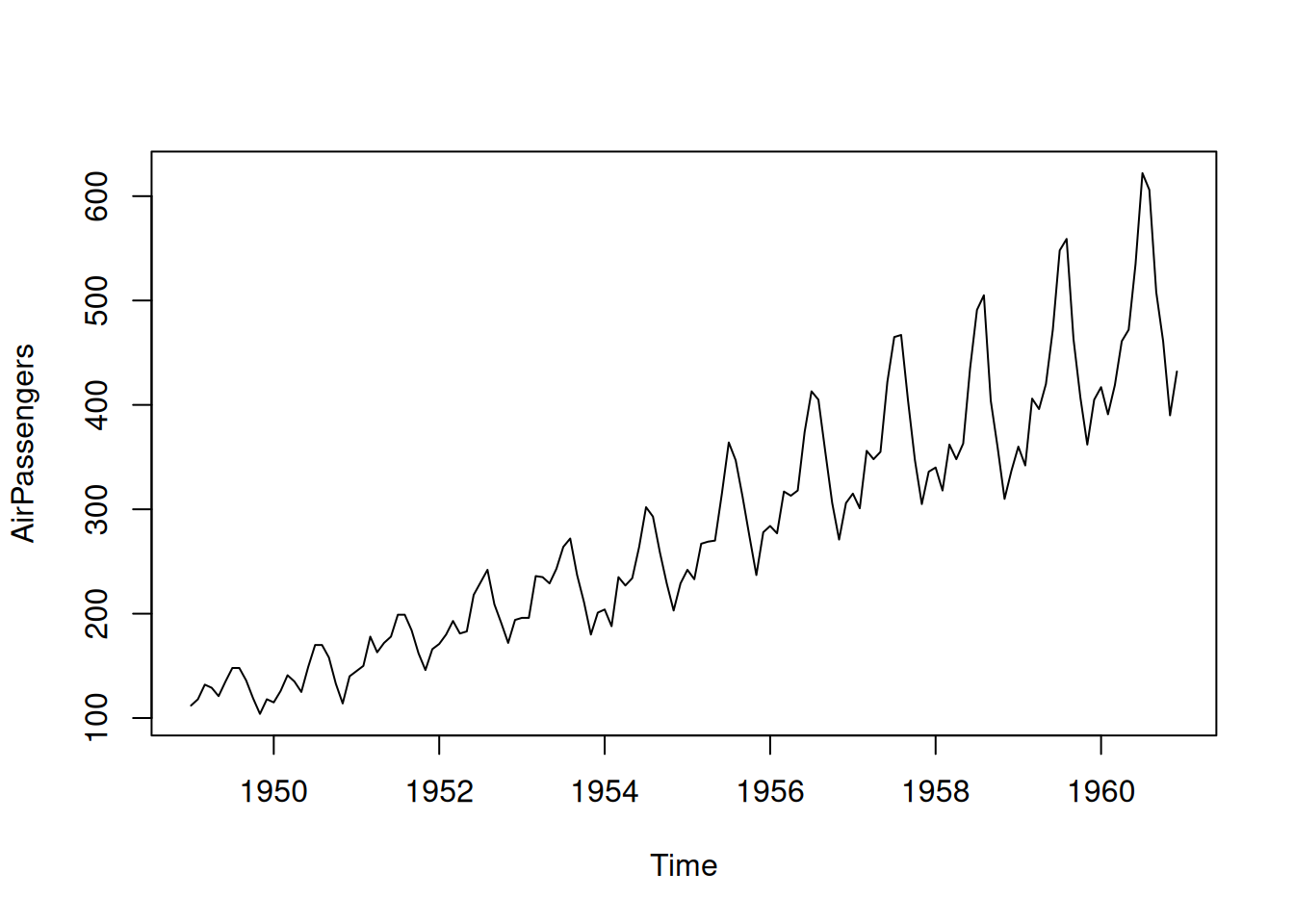
plot(rec, ylab='', xlab='', main='Recruitment')# Los clásicos datos de aerolíneas de Box & Jenkins.
# Totales mensuales de pasajeros internacionales, de 1949 a 1960.
plot(AirPassengers)8 DESCOMPOSICIÓN ESTACIONAL: ADITIVA Y MULTIPLICATIVA
Se realizan descomposiciones estacionales clásicas para identificar componentes como tendencia y estacionalidad.
require(graphics)
par(mfrow=c(1,1))
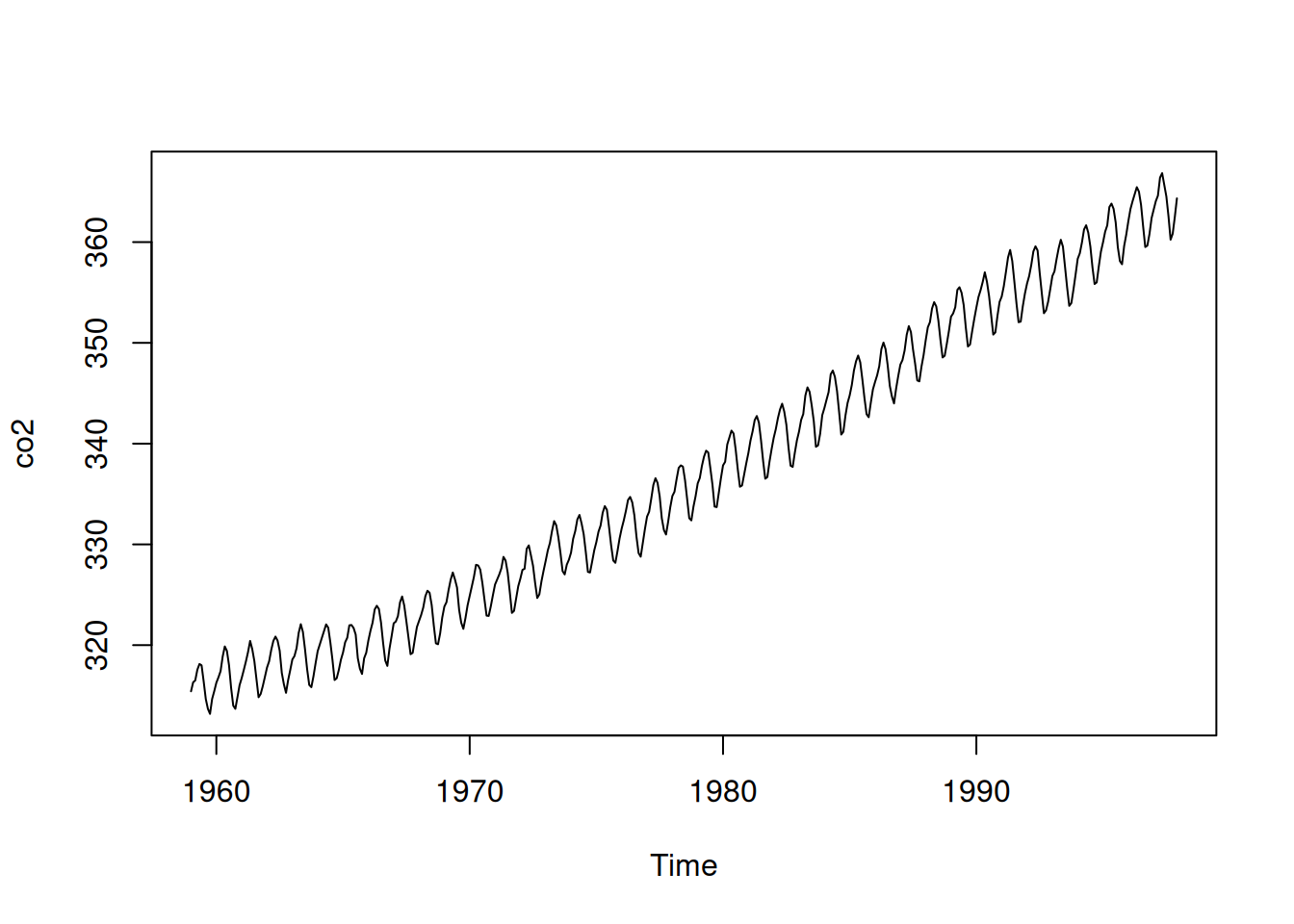
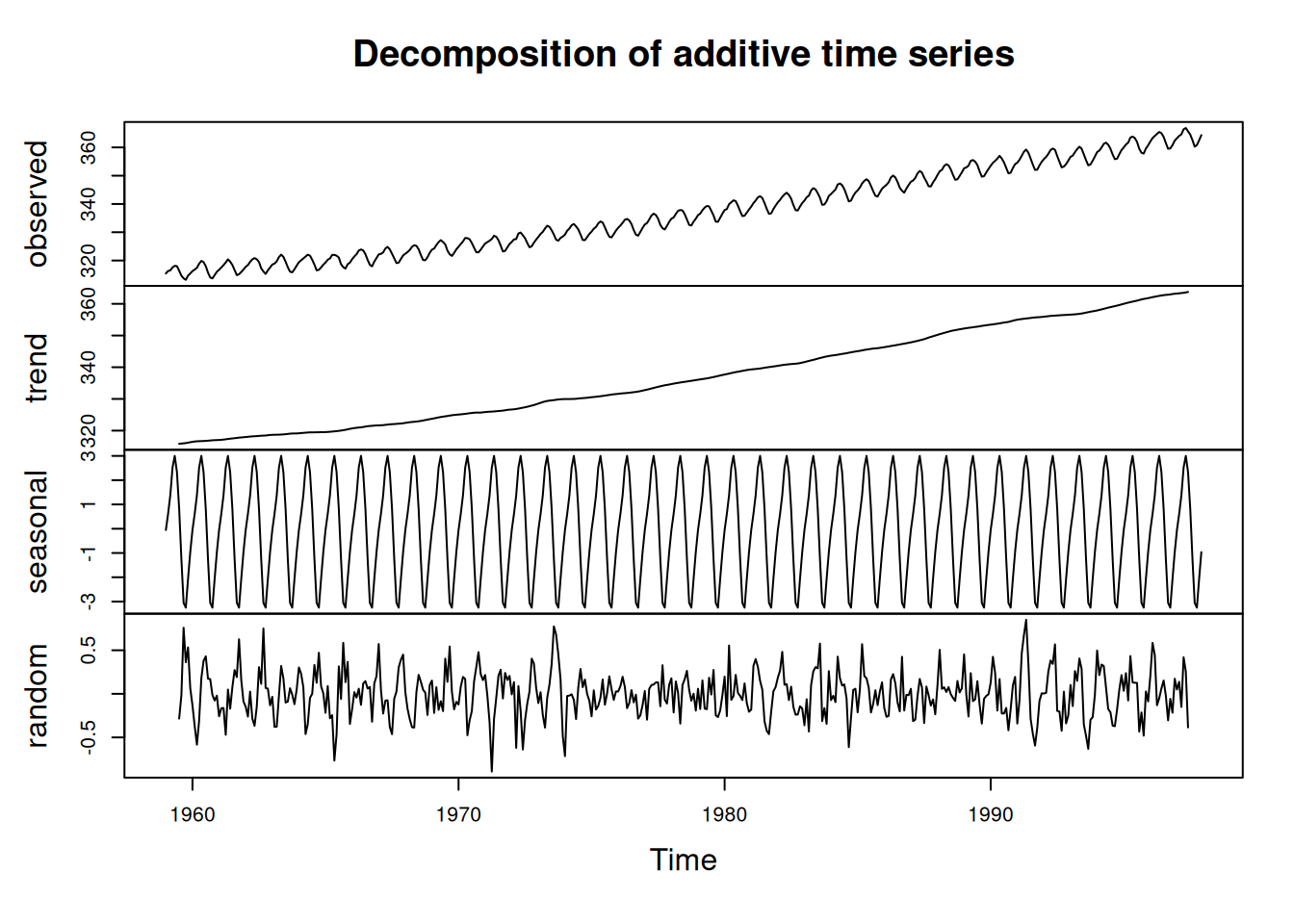
plot(co2, type="l")m <- decompose(co2, type="additive")
plot(m) # Grafica datos, tendencia, estacionalidad y error# Tarea: 1. Estudiar este tipo de descomposición
# 2. Investigar con qué métodos se puede extraer el ciclo de una serie.
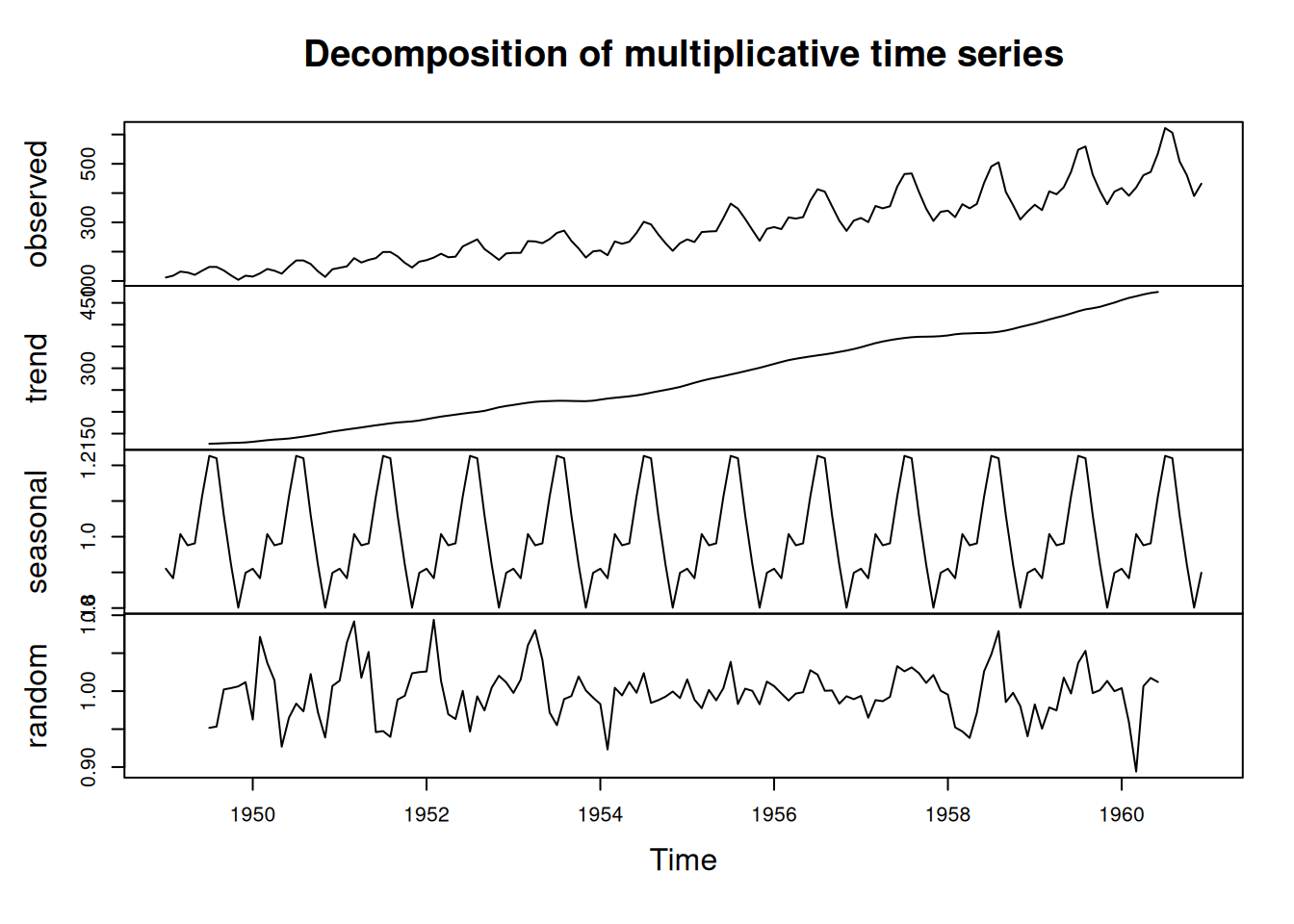
par(mfrow=c(1,1))
plot(AirPassengers)m <- decompose(AirPassengers, type="multiplicative")
plot(m)9 SIMULACIÓN DE SERIES DE TIEMPO
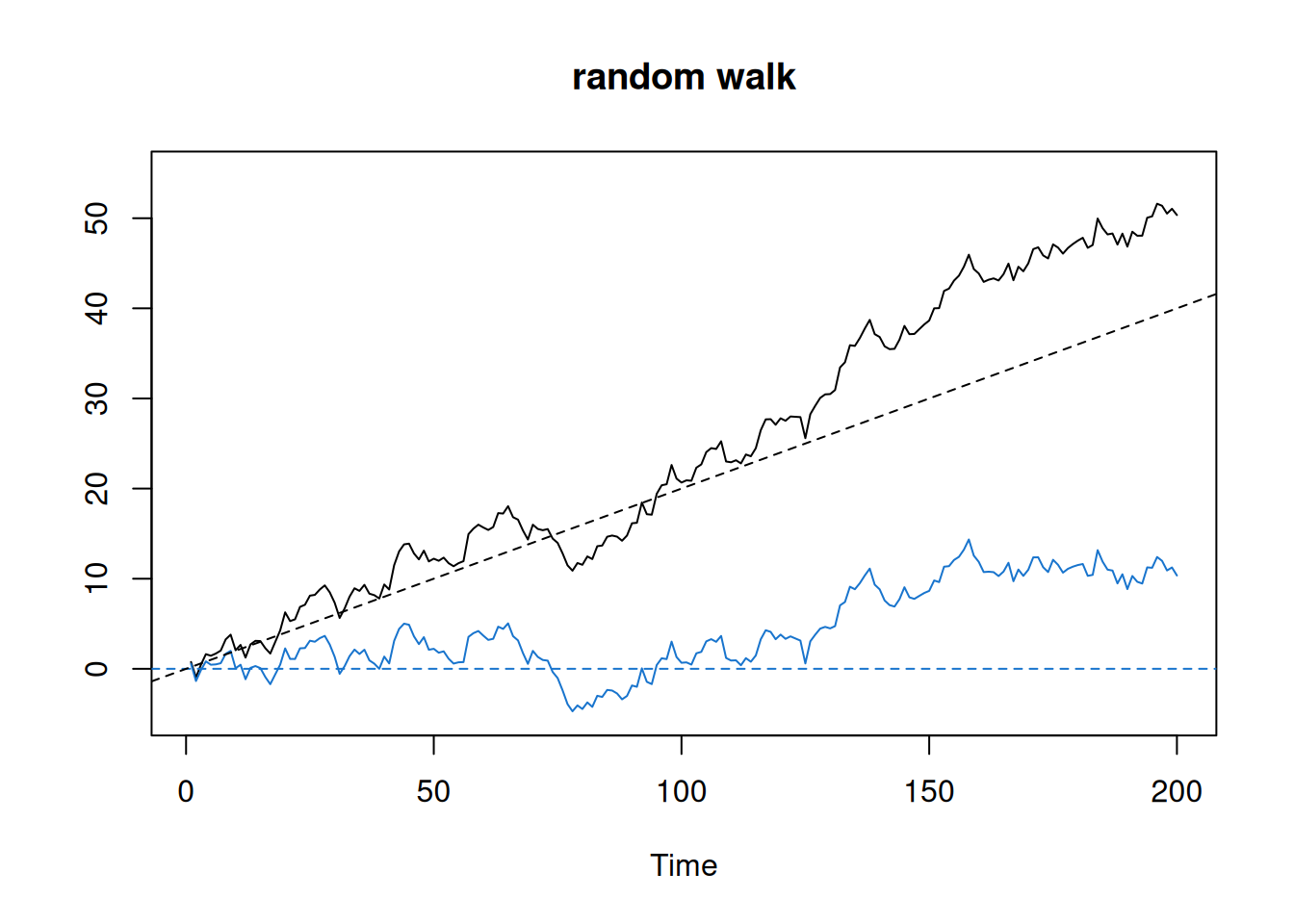
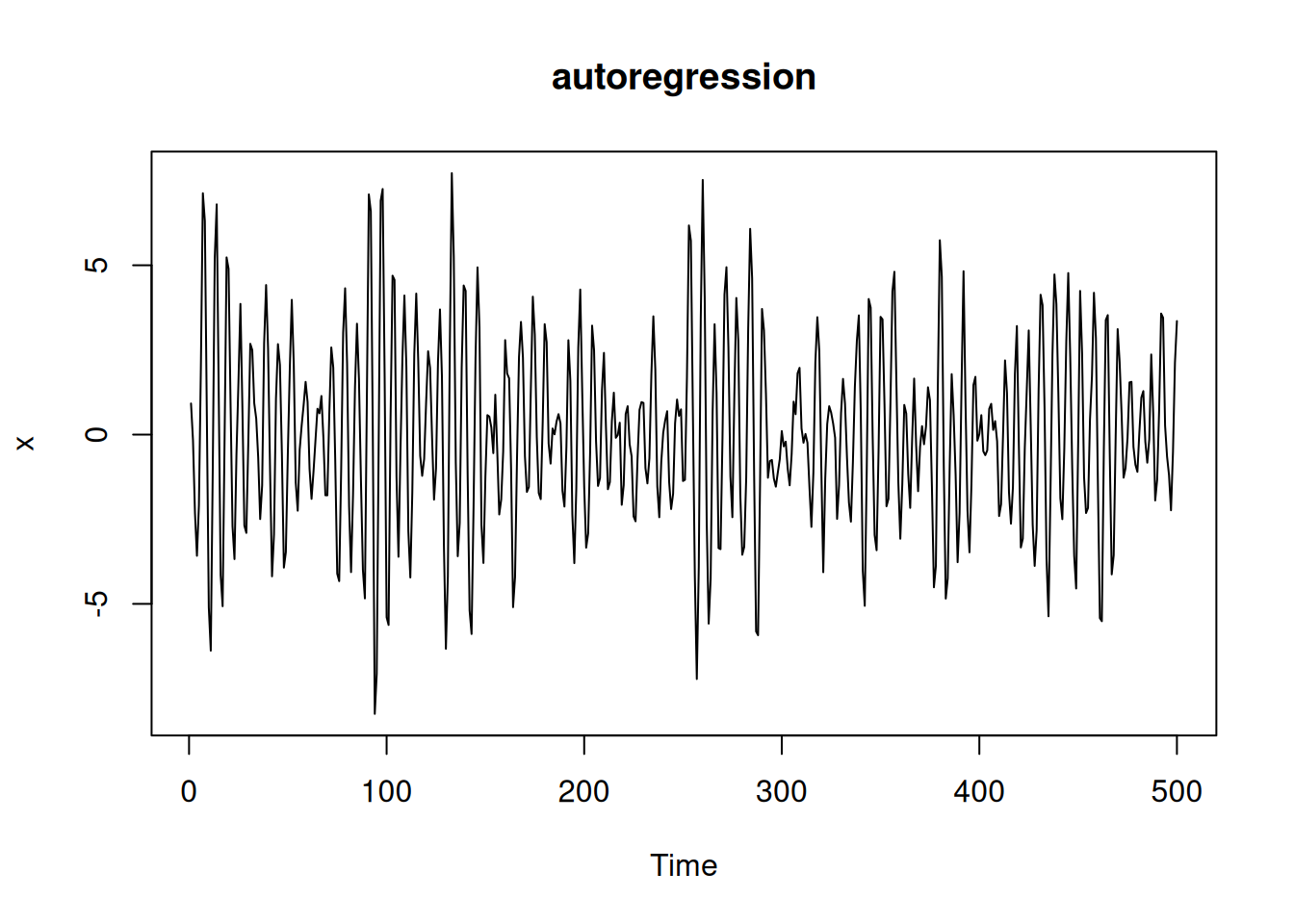
Se simulan distintos procesos: ruido blanco, caminata aleatoria y modelo AR(2).
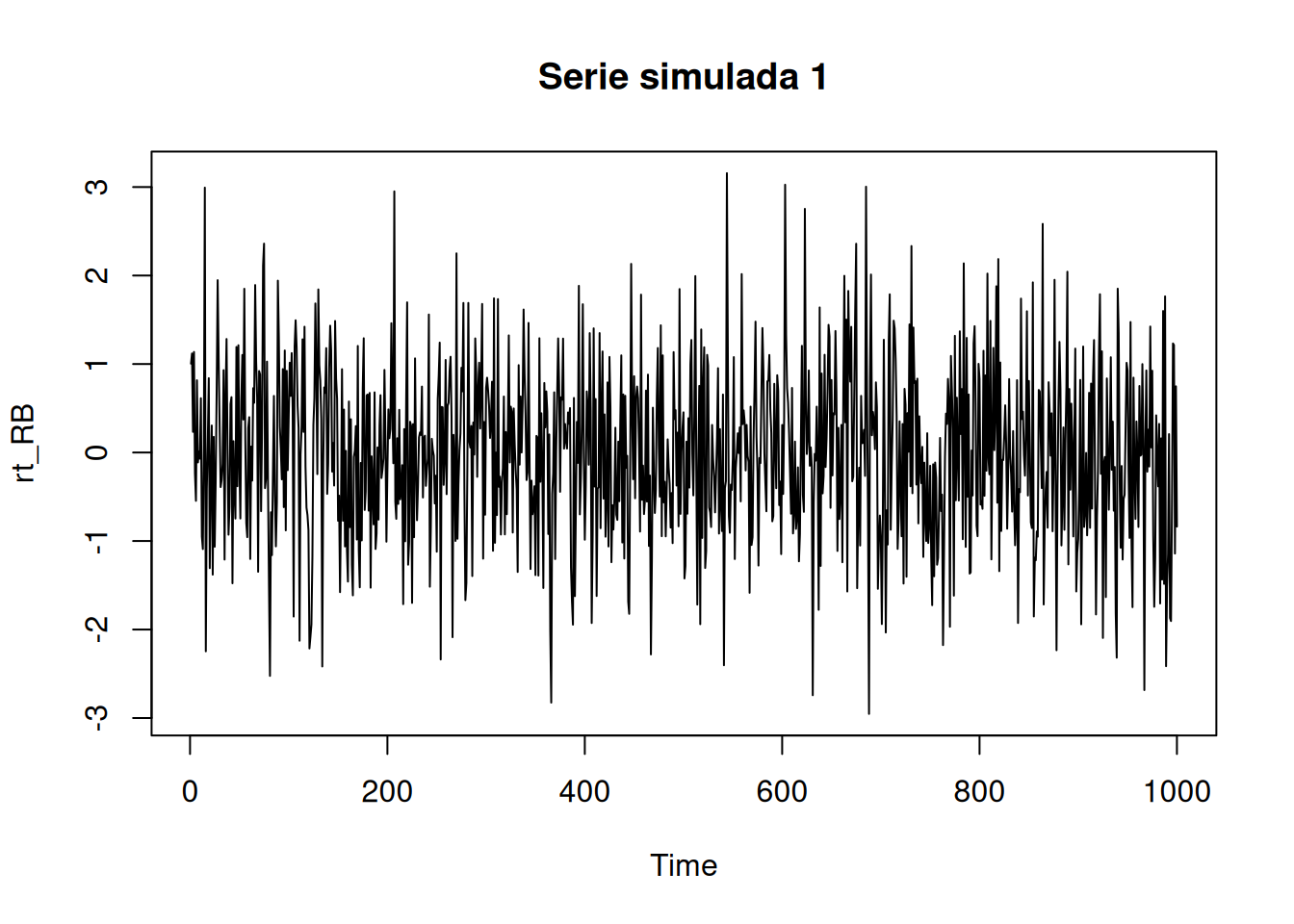
9.1 Ruido Blanco
rt_RB <- arima.sim(list(order=c(0,0,0)), n=1000 )
# El primer 0 es el componente autorregresivo, el segundo 0 se explicará luego y el tercer 0 indica el orden de la media móvil (cantidad de datos usados)
par(mfrow=c(1,1))
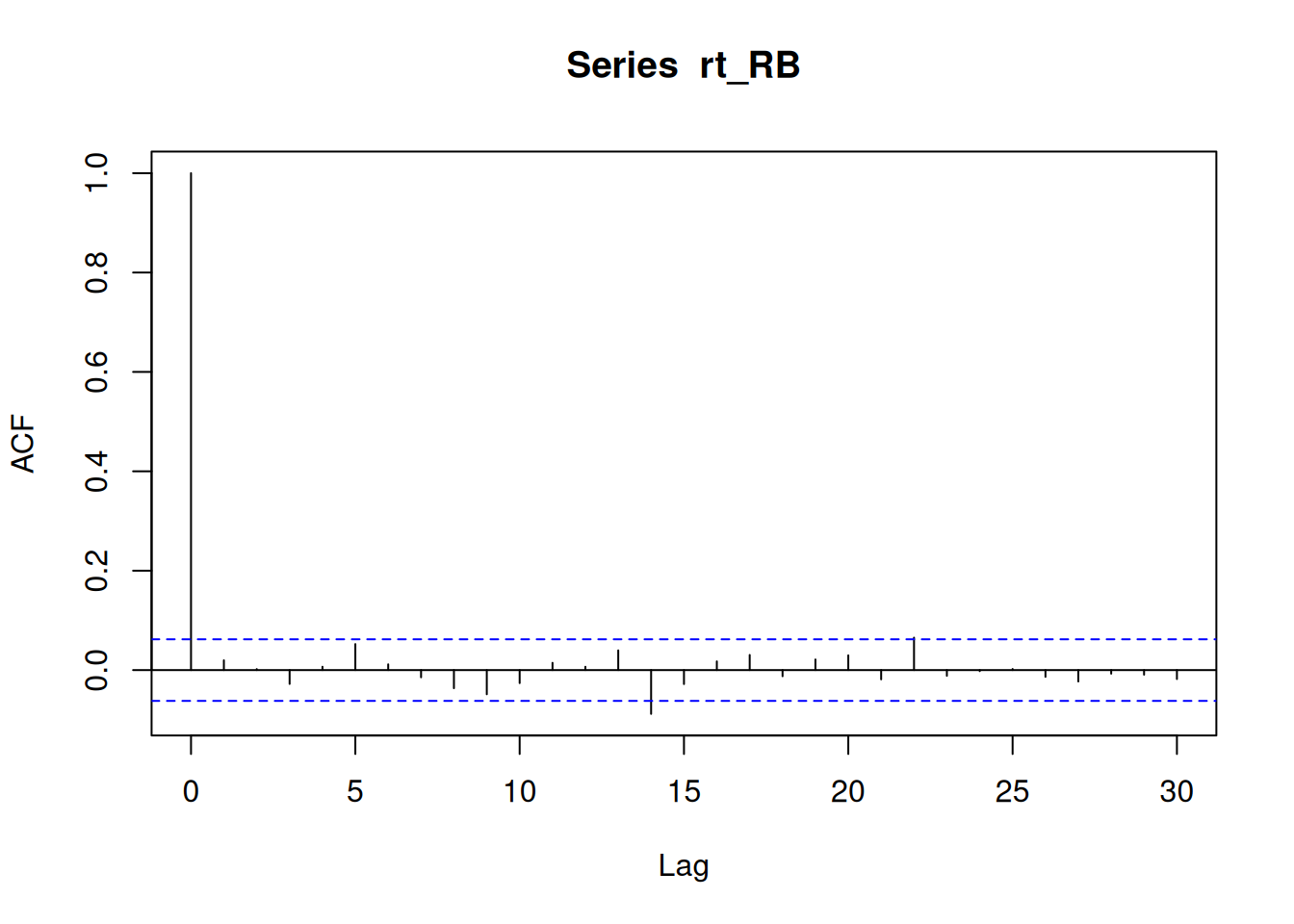
plot(rt_RB, type="l", main="Serie simulada 1")par(mfrow=c(1,1))
acf(rt_RB) # Función de autocorrelación muestral# Muestra la correlación entre -1 y 1; en un ruido blanco se espera que solo la autocorrelación en el retardo 0 sea significativa (valor 1)