library(tsoutliers)
library(forecast)13 Outliers e Intervención
13.1 Outliers en Modelos ARIMA
Vamos a considerar el análisis de outliers para modelos ARIMA o SARIMA.
La base fundamental del análisis de outliers se basa en en análisis de intervención. Vamos a empezar con unos ejercicios de simulación. La librería base es tsoutliers.
###### Simulación Outlier aditivo
set.seed(12)
n=200
serie=arima.sim(n=n,list(ar=(0.5))) #Se genera un AR(1)
serie2=serie
serie2[50]=serie2[50]-6 #En el dato 50, se le quitan 6 unidades para volverlo un outlier
par(mfrow=c(1,2))
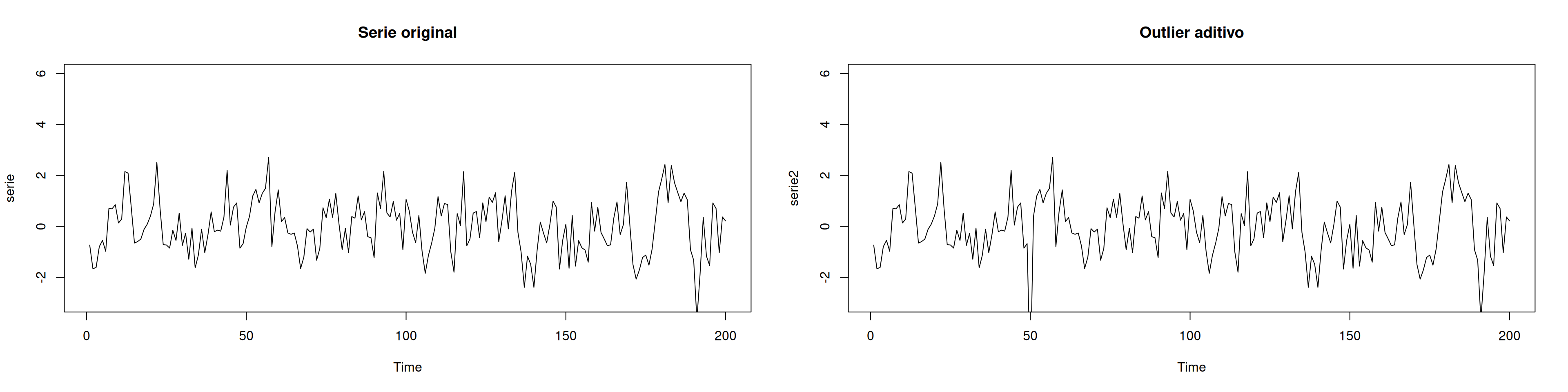
plot(serie,ylim=c(-3,6),main="Serie original")
plot(serie2,ylim=c(-3,6),main="Outlier aditivo")Después de simular un outlier aditivo en el tiempo \(t=50\) con impacto de 6, basada en una serie que proviene de de un modelo AR con \(\phi=0.5\).
En seguida vamos ajustar los modelos a las series con y sin outlier vía el procedimiento automático.
auto.arima(serie2)###Ajuste para el modelo con outlierSeries: serie2
ARIMA(1,0,0) with zero mean
Coefficients:
ar1
0.4119
s.e. 0.0642
sigma^2 = 1.117: log likelihood = -294.44
AIC=592.88 AICc=592.94 BIC=599.48#Se observa que cambió la estimación por no tener en cuenta el dato atípico para modelar
auto.arima(serie)###Ajuste para el modelo sin outlier Series: serie
ARIMA(1,0,0) with zero mean
Coefficients:
ar1
0.4693
s.e. 0.0622
sigma^2 = 0.9065: log likelihood = -273.6
AIC=551.2 AICc=551.26 BIC=557.79fit= arima(serie2,order=c(1,0,0),include.mean = F)
fit
Call:
arima(x = serie2, order = c(1, 0, 0), include.mean = F)
Coefficients:
ar1
0.4119
s.e. 0.0642
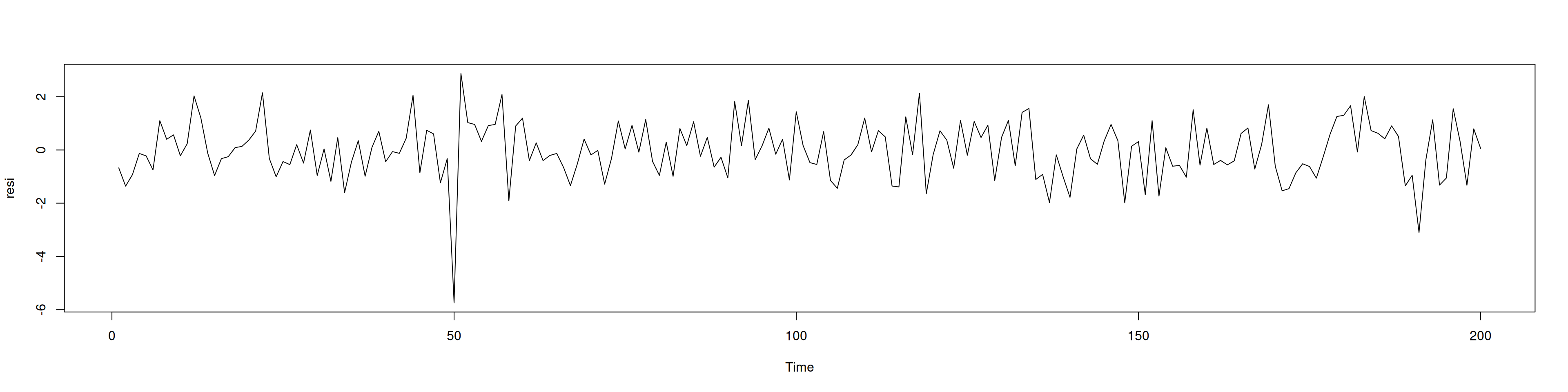
sigma^2 estimated as 1.111: log likelihood = -294.44, aic = 592.88resi= residuals(fit)
plot(resi)#Se observa en la gráfica de los residuales el efecto de no tener en cuenta los datos típicosNote que el residual correspodiente a la observación 50 es bastante grande.
13.2 Detección de outliers: procedimiento automático
coef= coefs2poly(fit)
coef$arcoefs
[1] 0.4119239
$macoefs
numeric(0)
attr(,"class")
[1] "ArimaPars"outliers= tsoutliers::locate.outliers(resi,coef) #Inidca el tipo de dato atípico, la posición y su efecto.
outliers###tstat se compara con C=3 type ind coefhat tstat
1 AO 50 -5.924796 -6.44878# ?tso####Detección automática de outliers, donde el modelo que se propone es via auto.arima
tso(serie2) #Otra forma de ver el efecto de los outliers. Pero no lo tiene en cuenta para calcular el coeficienteSeries: serie2
Regression with ARIMA(1,0,0) errors
Coefficients:
ar1 AO50
0.4693 -5.9156
s.e. 0.0622 0.8598
sigma^2 = 0.9111: log likelihood = -273.59
AIC=553.19 AICc=553.31 BIC=563.08
Outliers:
type ind time coefhat tstat
1 AO 50 50 -5.916 -6.8813.3 Simulación Outlier cambio de nivel
set.seed(12)
n=500
serie=arima.sim(n=n,list(ar=0.3))
serie2=serie
serie2[100:n]=serie2[100:n]+4 #A partir del dato 100, se mete un cambio de nivel de impactó 4
par(mfrow=c(1,2))
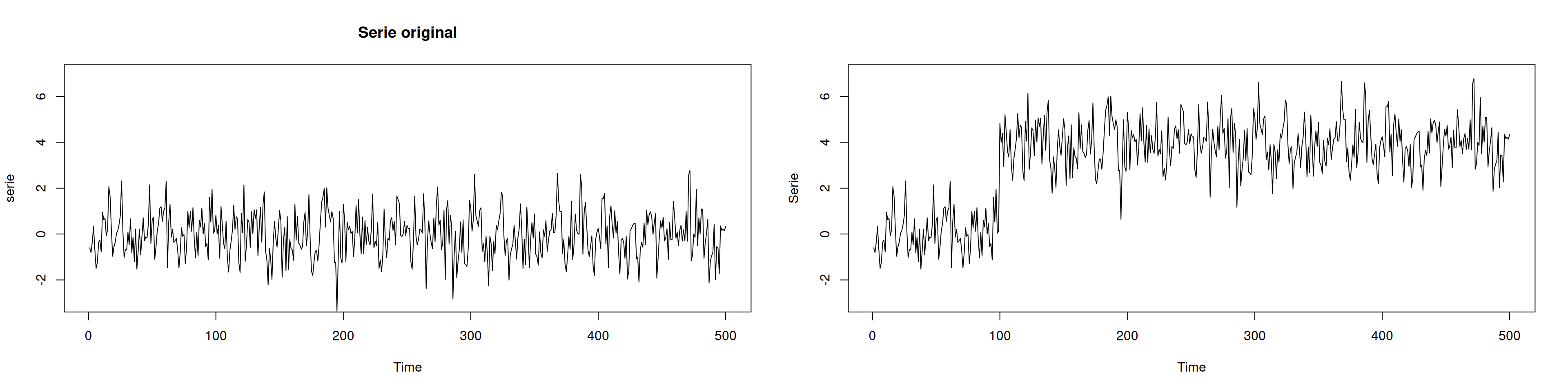
plot(serie,ylim=c(-3,7),main="Serie original")
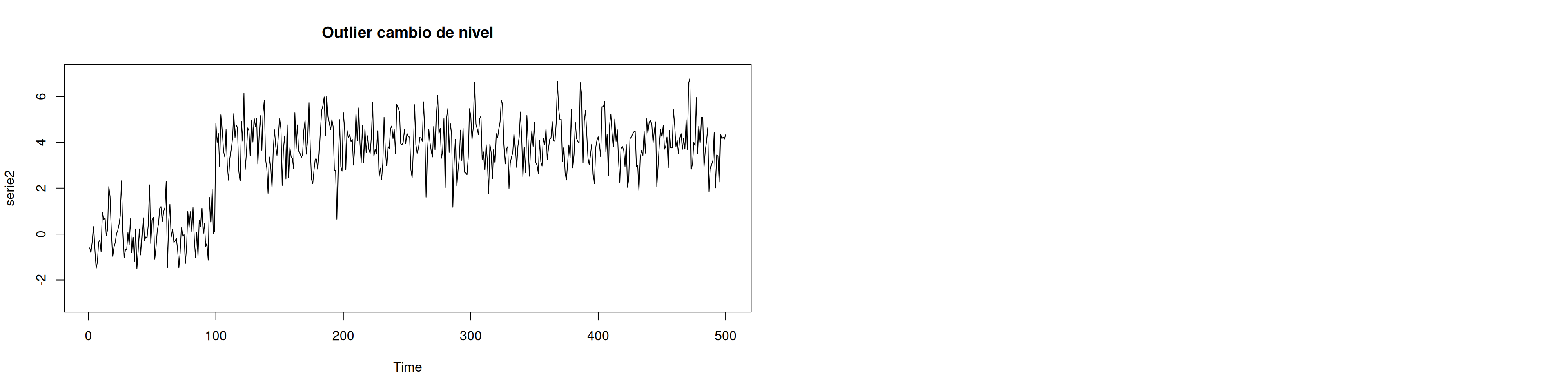
plot(serie2,ylim=c(-3,7),ylab="Serie")plot(serie2,ylim=c(-3,7),main="Outlier cambio de nivel")fit= Arima(serie2,order=c(1,0,0),include.mean = F)
fit # Se ve el apalancamientoSeries: serie2
ARIMA(1,0,0) with zero mean
Coefficients:
ar1
0.9455
s.e. 0.0142
sigma^2 = 1.421: log likelihood = -797.88
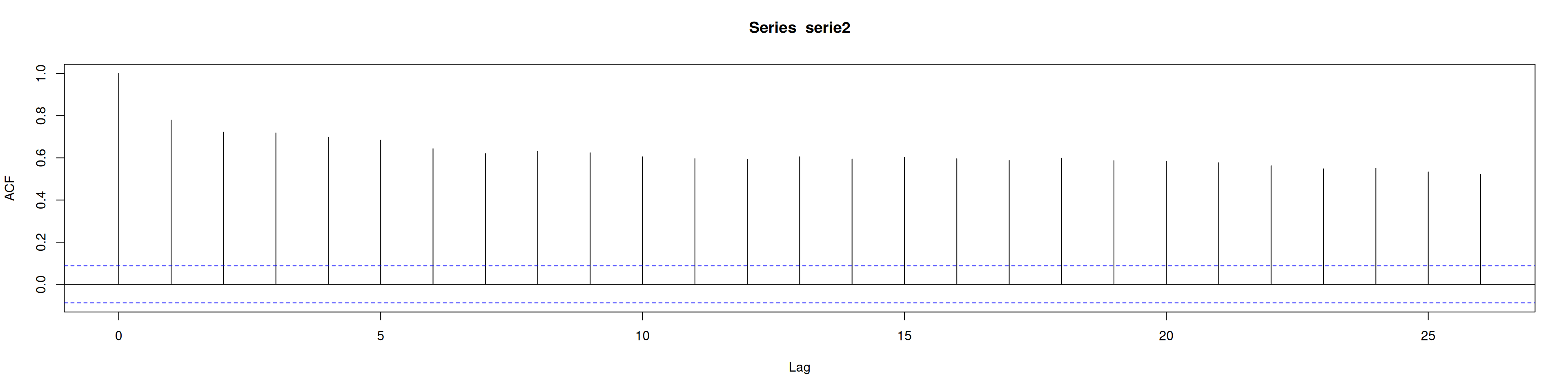
AIC=1599.75 AICc=1599.78 BIC=1608.18acf(serie2) #El apalancamiento fue tan grande que hace que la serie parezca estacional, cuando no es estacionariaresi= residuals(fit)
coef= coefs2poly(fit)
outliers= locate.outliers(resi,coef,cval=5)###cval=3.5 por defecto
outliers type ind coefhat tstat
1 LS 100 4.290489 5.558564xreg = outliers.effects(outliers, n) #Es la intervención que creabamos en el punto anterior, genera una variable escalón
head(xreg); tail(xreg) LS100
[1,] 0
[2,] 0
[3,] 0
[4,] 0
[5,] 0
[6,] 0 LS100
[495,] 1
[496,] 1
[497,] 1
[498,] 1
[499,] 1
[500,] 1#tso(serie2)
#salida_tso=tso(y=serie2,types=c("LS"))
#plot(salida_tso$yadj)####Esta serie es sin el efecto de los outliers
#plot(tso(y=serie2,types=c("LS")))
#tso(y=serie2,xreg=xreg,tsmethod="arima",args.tsmethod=list(include.mean=FALSE,order=c(1,0,0)))#####Yo especifico el modelo
fit_2=Arima(serie2,order=c(1,0,0),xreg=xreg,include.mean = F)
resi_2= residuals(fit_2)
coef_2= coefs2poly(fit_2)
outliers_2= locate.outliers(resi_2,coef_2,cval=3.5)###cval=3.5 por defecto
outliers_2 #Verifico que se haya solucionado el problem de los outliers[1] type ind coefhat tstat
<0 rows> (or 0-length row.names)####Hay que repetir el análisis de residuales del modelo.13.4 Pronóstico con outliers
Para el pronóstico, debo tener en cuenta los valores futuros de la variable de intervención.
##### Pronóstico
#fit= Arima(serie2,order=c(1,0,0),include.mean = F)
fit2= Arima(serie2,order=c(1,0,0),include.mean = F,xreg=xreg)
#pronostico= forecast(object=fit,h=15) #4.093698
regresoras=c(rep(1,15))
pronostico_out=forecast(object=fit2,xreg=regresoras,h=15) Warning in forecast.forecast_ARIMA(object = fit2, xreg = regresoras, h = 15):
xreg contains different column names from the xreg used in training. Please
check that the regressors are in the same order.#par(mfrow=c(1,2))
#plot(pronostico,ylim=c(-3,7))
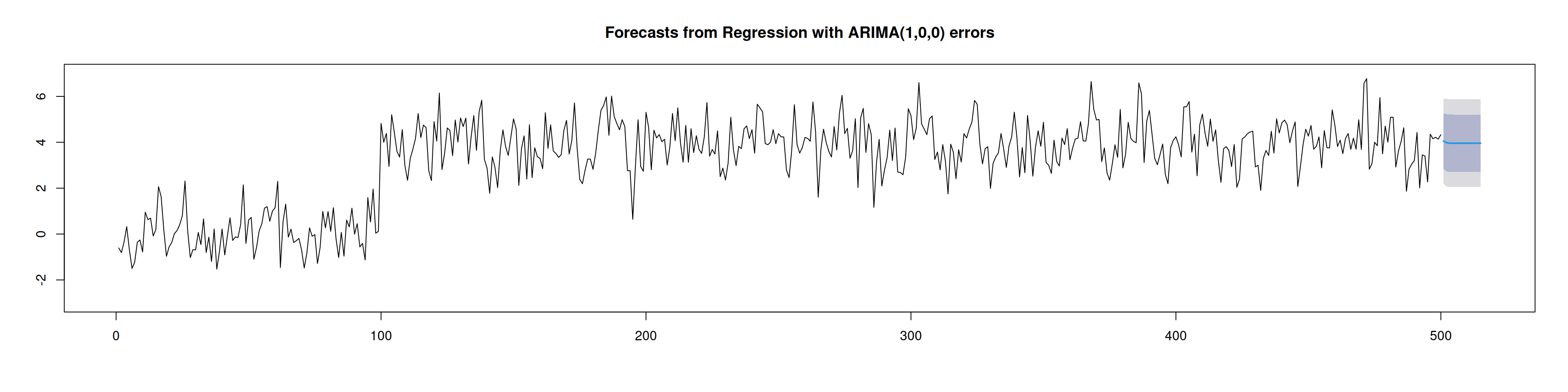
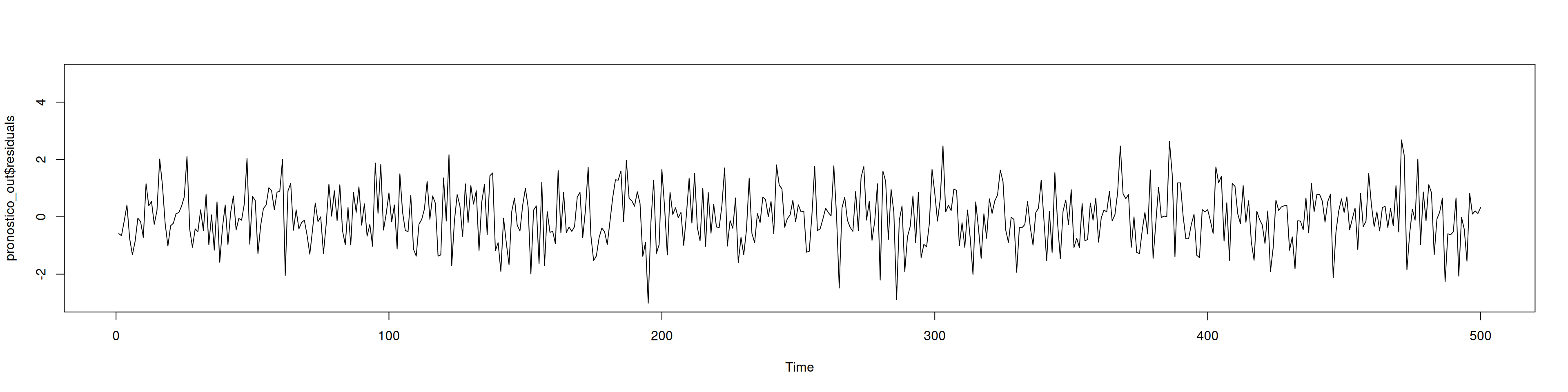
plot(pronostico_out,ylim=c(-3,7)) ###Note la reducción en la varianza de las predicciones #plot(pronostico$residuals,ylim=c(-3,5))
plot(pronostico_out$residuals,ylim=c(-3,5)) #El prónostico ya tuvo en cuenta el dato atípico13.5 Ejemplo Serie de Pasajeros
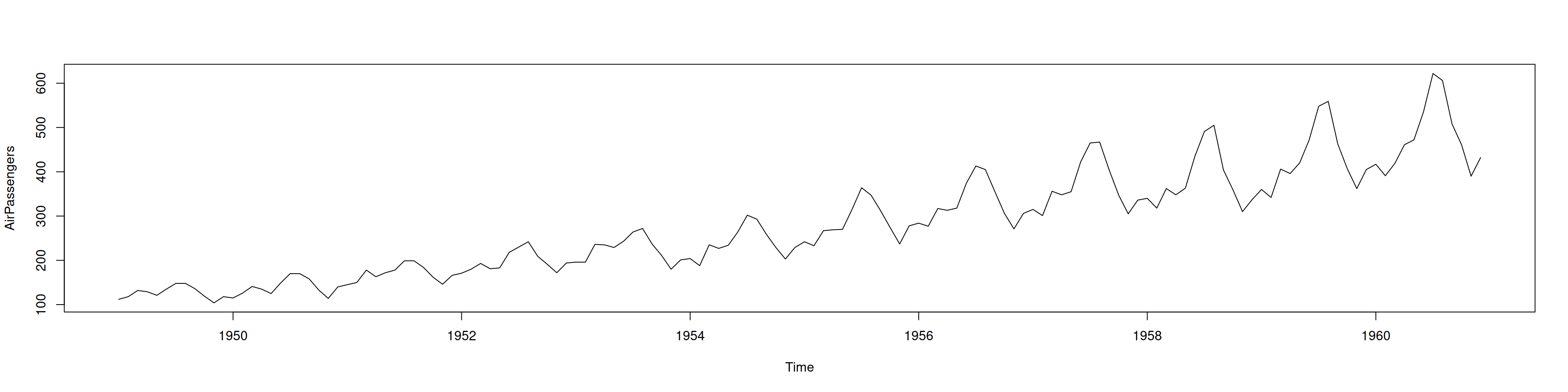
library(lmtest)data("AirPassengers")
plot(AirPassengers)serie <- AirPassengers
ajuste=Arima(serie,order=c(0,1,1),seasonal = list(order = c(0, 1, 1)),include.mean=F,lambda =0 )
# lambda = 0 le añade el logaritmo a la serie
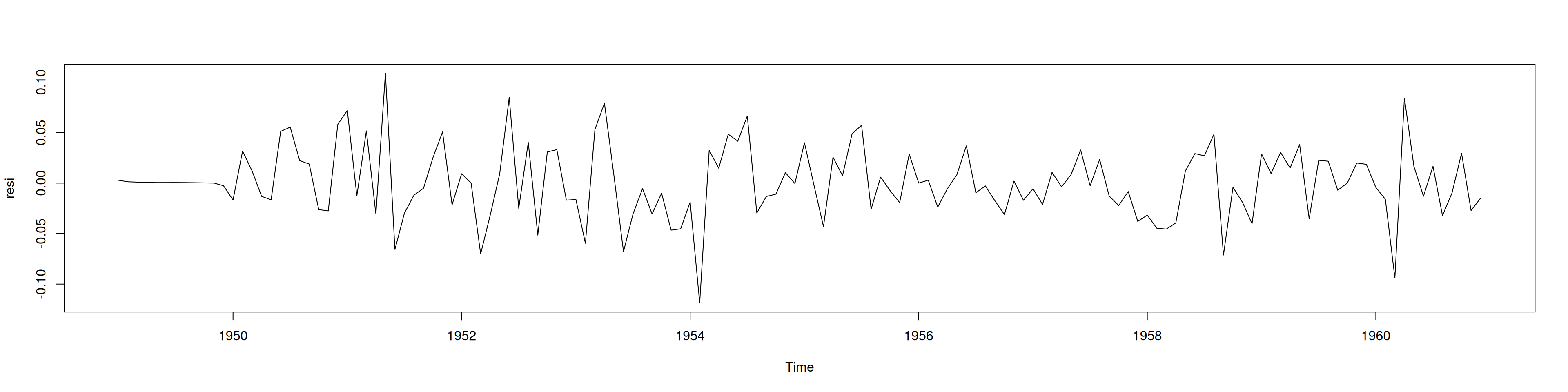
resi= residuals(ajuste)
plot(resi)coef= coefs2poly(ajuste)
outliers= locate.outliers(resi,coef)
outliers type ind coefhat tstat
1 AO 29 0.08716944 3.736147
2 AO 62 -0.08410177 -3.604320
3 AO 135 -0.10318382 -3.902051n=length(serie)
xreg = outliers.effects(outliers,n )
head(xreg); tail(xreg) AO29 AO62 AO135
[1,] 0 0 0
[2,] 0 0 0
[3,] 0 0 0
[4,] 0 0 0
[5,] 0 0 0
[6,] 0 0 0 AO29 AO62 AO135
[139,] 0 0 0
[140,] 0 0 0
[141,] 0 0 0
[142,] 0 0 0
[143,] 0 0 0
[144,] 0 0 0###El siguiente procedimiento busca que al ajustar, en el modelo con el efecto de los outliers, se busquen si hay mas outliers.
analisis=Arima(serie,order=c(0,1,1),seasonal = list(order = c(0, 1, 1)),include.mean=F,lambda =0 ,xreg=xreg) #xreg contiene las tres dummies aditivas
analisisSeries: serie
Regression with ARIMA(0,1,1)(0,1,1)[12] errors
Box Cox transformation: lambda= 0
Coefficients:
ma1 sma1 AO29 AO62 AO135
-0.2898 -0.5246 0.0893 -0.0804 -0.1034
s.e. 0.0990 0.0746 0.0228 0.0226 0.0257
sigma^2 = 0.001067: log likelihood = 263.03
AIC=-514.06 AICc=-513.38 BIC=-496.81coeftest(analisis)
z test of coefficients:
Estimate Std. Error z value Pr(>|z|)
ma1 -0.289774 0.098960 -2.9282 0.003410 **
sma1 -0.524605 0.074572 -7.0349 1.994e-12 ***
AO29 0.089326 0.022818 3.9148 9.049e-05 ***
AO62 -0.080432 0.022571 -3.5635 0.000366 ***
AO135 -0.103417 0.025710 -4.0225 5.759e-05 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1resi_analisis= residuals(analisis)
coef_analisis= coefs2poly(analisis)
outliers_analisis= locate.outliers(resi_analisis,coef_analisis)
outliers_analisis # Verficar outliers, me aparece un nuevo otlier de cambio de nivel type ind coefhat tstat
1 LS 54 -0.09604727 -3.923821xreg_analisis = outliers.effects(outliers_analisis,n )
####Se pone "AO" en types porque en la localización de outliers únicamente encontró aditivos. Se incluye los efectos de los outliers, así que ahora encontró un outlier cambio de nivel en el tiempo 54.
total_outliers=cbind(xreg,xreg_analisis)
analisis_final=Arima(serie,order=c(0,1,1),seasonal = list(order = c(0, 1, 1)),include.mean=F,lambda =0 ,xreg=total_outliers)
analisis_finalSeries: serie
Regression with ARIMA(0,1,1)(0,1,1)[12] errors
Box Cox transformation: lambda= 0
Coefficients:
ma1 sma1 AO29 AO62 AO135 LS54
-0.3320 -0.4965 0.0959 -0.0803 -0.1032 -0.0967
s.e. 0.0909 0.0759 0.0218 0.0216 0.0248 0.0249
sigma^2 = 0.0009703: log likelihood = 270.03
AIC=-526.06 AICc=-525.15 BIC=-505.93coeftest(analisis_final) # Como todos los outliers son significativos se dejan todos
z test of coefficients:
Estimate Std. Error z value Pr(>|z|)
ma1 -0.332037 0.090947 -3.6509 0.0002613 ***
sma1 -0.496497 0.075884 -6.5428 6.038e-11 ***
AO29 0.095898 0.021830 4.3930 1.118e-05 ***
AO62 -0.080318 0.021587 -3.7207 0.0001986 ***
AO135 -0.103224 0.024815 -4.1598 3.186e-05 ***
LS54 -0.096727 0.024888 -3.8865 0.0001017 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1resi_final= residuals(analisis_final)
coef_final= coefs2poly(analisis_final)
outliers_final= locate.outliers(resi_final,coef_final)
outliers_final[1] type ind coefhat tstat
<0 rows> (or 0-length row.names)###No se encontraron mas outliers
###Verificar los supuestos del modelo.###Creación de las variable de intervención
pasos_adel=12
num_outliers=dim(total_outliers)[2]
regresoras_aditivos=matrix(c(rep(0,pasos_adel*(num_outliers-1))),pasos_adel,num_outliers-1)
regresoras_LS=matrix(c(rep(1,pasos_adel)),pasos_adel,1)
regresoras=cbind(regresoras_aditivos,regresoras_LS)
colnames(regresoras)=colnames(total_outliers)
pronostico_out=forecast(object=analisis_final,xreg=regresoras,h=pasos_adel)
pronostico_out Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
Jan 1961 449.8404 432.2367 468.1610 423.1985 478.1595
Feb 1961 424.7048 404.7981 445.5905 394.6407 457.0593
Mar 1961 500.6276 473.8772 528.8880 460.3000 544.4884
Apr 1961 492.0941 462.9524 523.0702 448.2309 540.2497
May 1961 508.9298 476.1319 543.9870 459.6342 563.5124
Jun 1961 582.3461 542.0245 625.6673 521.8223 649.8898
Jul 1961 670.5677 621.1525 723.9140 596.4852 753.8510
Aug 1961 666.7261 614.8142 723.0213 588.9904 754.7215
Sep 1961 556.8647 511.3170 606.4696 488.7336 634.4934
Oct 1961 497.1427 454.6262 543.6352 433.6116 569.9820
Nov 1961 428.9600 390.7509 470.9052 371.9219 494.7454
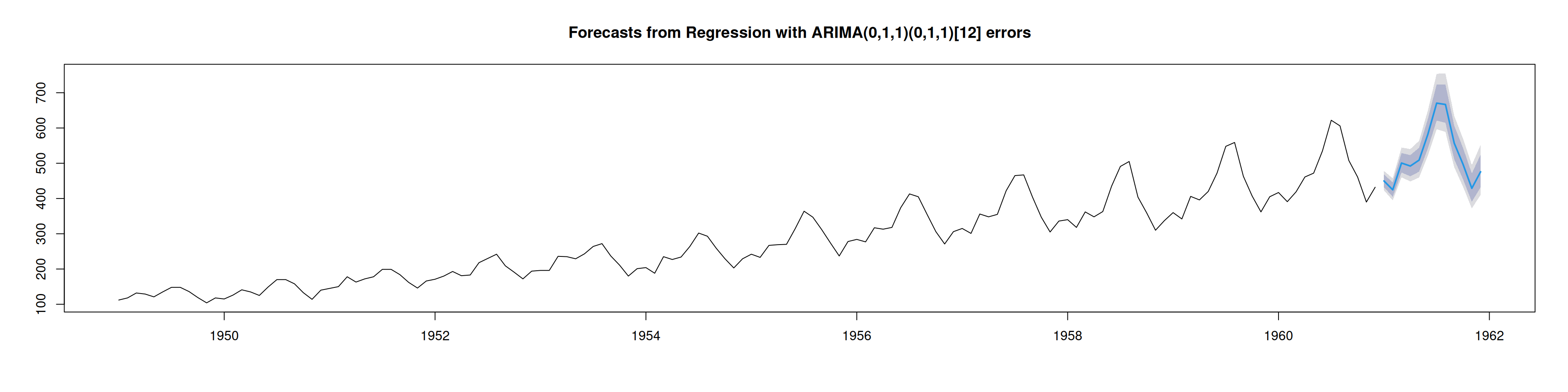
Dec 1961 475.9017 431.8949 524.3925 410.2711 552.0311plot(pronostico_out)#Primero se ajusta el modelo y después se busca outliers