set.seed(123)
sim_data <- arima.sim(n = 100, list(order = c(1, 1, 1), ar = 0.5, ma = 0.5))
# Ajustar a 100 observaciones
sim_data <- sim_data[-1]
layout(matrix(c(1,1,2, 1,1,3), nc=2))
par(mar = c(3,3,2,1), mgp = c(1.6, .6, 0))
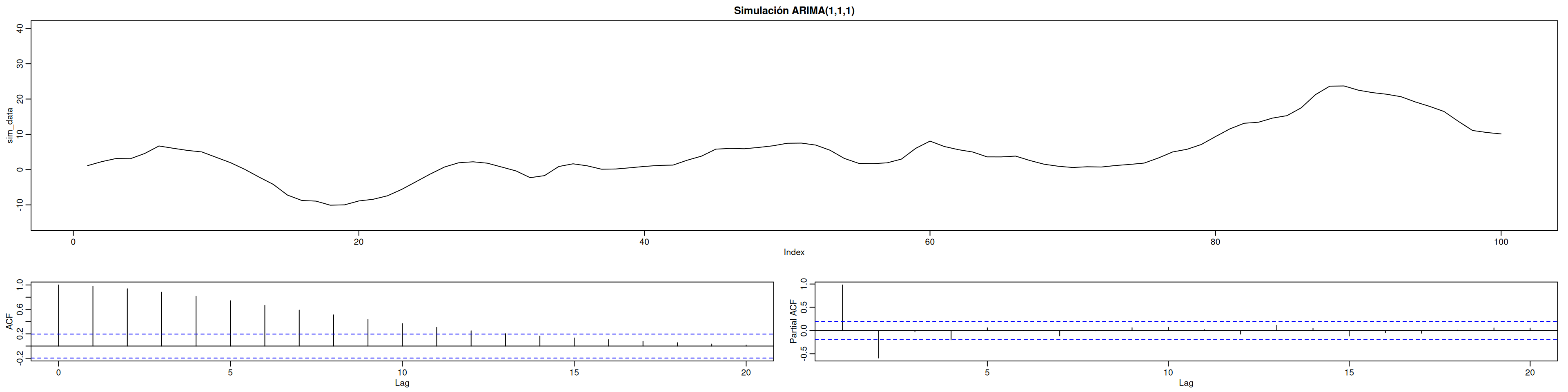
plot(sim_data, type="l", ylim = c(-15,40), main = "Simulación ARIMA(1,1,1)")
acf(sim_data, main = "ACF de la serie simulada")
pacf(sim_data, main = "PACF de la serie simulada")12 Intervención
12.1 Descripción del ejercicio
- Instalación y carga de los paquetes necesarios.
- Simulación de una serie ARIMA(1,1,1).
- Intervención puntual en \(t=50\).
- Ajuste de un ARIMA con variable de intervención (ARIMAX).
- Pronóstico incorporando la intervención.
- Visualización de resultados.
12.2 1. Instalación y carga
12.3 2. Simulación de la serie ARIMA(1,1,1)
Simulamos
\[
(1 - 0.5B)(1-B)Y_t = (1 + 0.5B)\,w_t
\] con \(n=100\).
Interpretación: ACF/PACF muestran decaimiento exponencial típico de ARMA con integración.
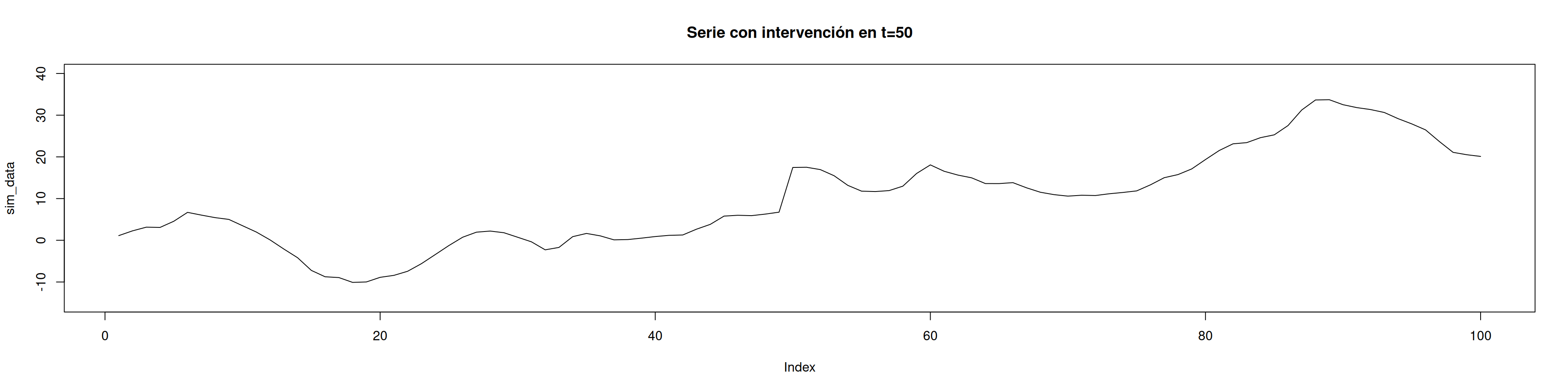
12.4 3. Introducción de la intervención
Creamos un dummy de paso en \(t=50\) y añadimos un salto de +10:
intervention <- rep(0, 100)
intervention[50:100] <- 1 #A partir del dato 50 lo vuelve 1
sim_data[50:100] <- sim_data[50:100] + 10 #sumar 10 a partir del datos 50 (es el tamaño del impacto)
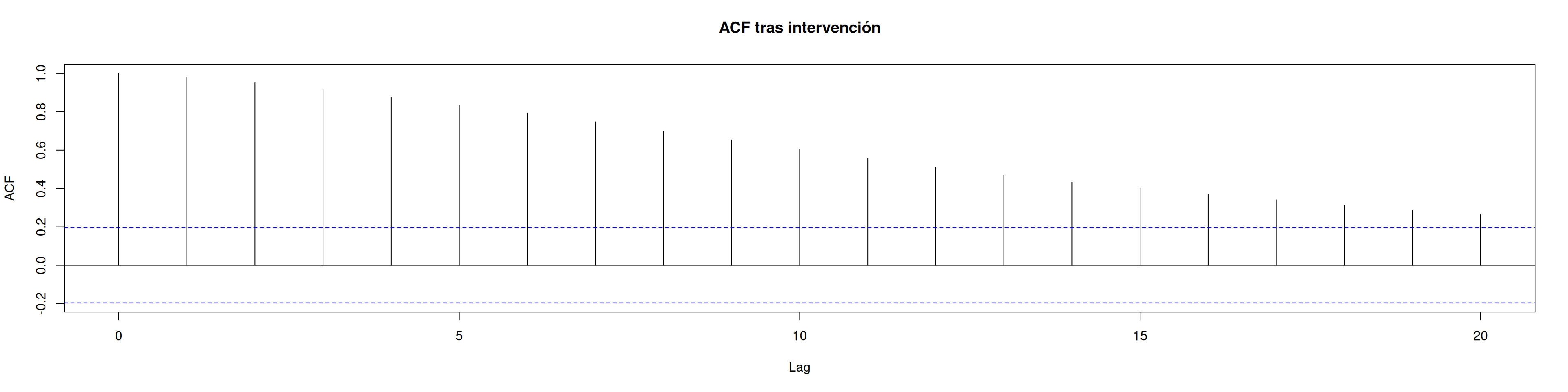
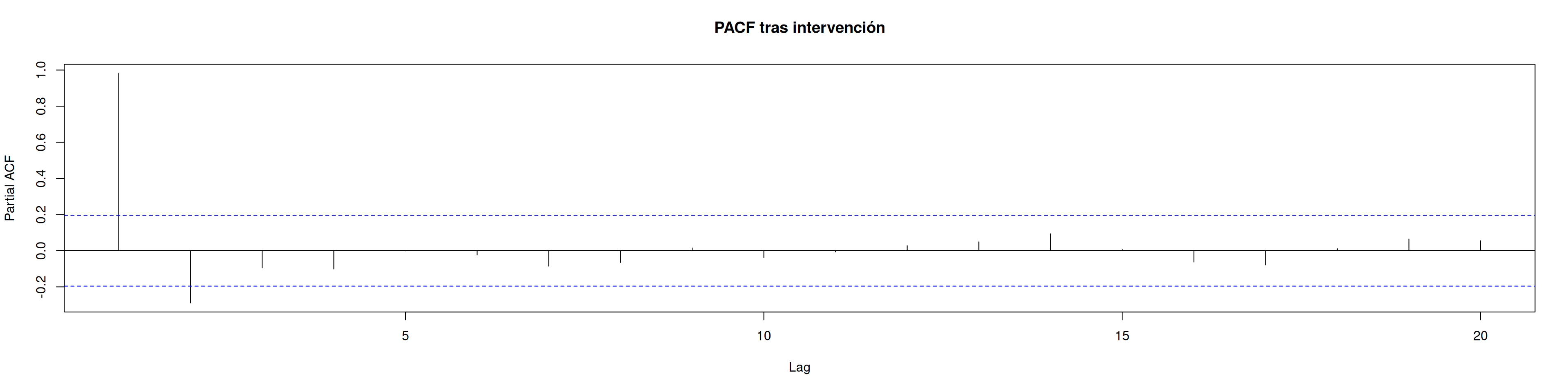
plot(sim_data, type="l", ylim = c(-15,40), main = "Serie con intervención en t=50")acf(sim_data, main = "ACF tras intervención")pacf(sim_data, main = "PACF tras intervención")12.5 4. Ajuste del modelo ARIMAX
Ajustamos
\[
Y_t = \text{ARIMA}(1,1,1) + \beta\,I_t + e_t
\] donde \(I_t\) es el dummy de intervención.
# Ajuste automático con regresor
model <- auto.arima(sim_data, xreg = intervention)
#Es importante ponerle el xreg, que es el outlier de escalon, o sino, cambia la dinámica de la serie
# Resultados del ajuste
summary(model)Series: sim_data
Regression with ARIMA(3,0,1) errors
Coefficients:
ar1 ar2 ar3 ma1 xreg
1.1219 0.1570 -0.3115 0.8960 9.7343
s.e. 0.1378 0.2398 0.1307 0.0969 0.5947
sigma^2 = 0.776: log likelihood = -129.76
AIC=271.53 AICc=272.43 BIC=287.16
Training set error measures:
ME RMSE MAE MPE MAPE MASE
Training set 0.1028105 0.8585763 0.6735272 -7.249047 30.30463 0.5587202
ACF1
Training set -0.01282896Interpretación: El coeficiente de intervention estima el efecto puntual (nivel) tras \(t=50\).
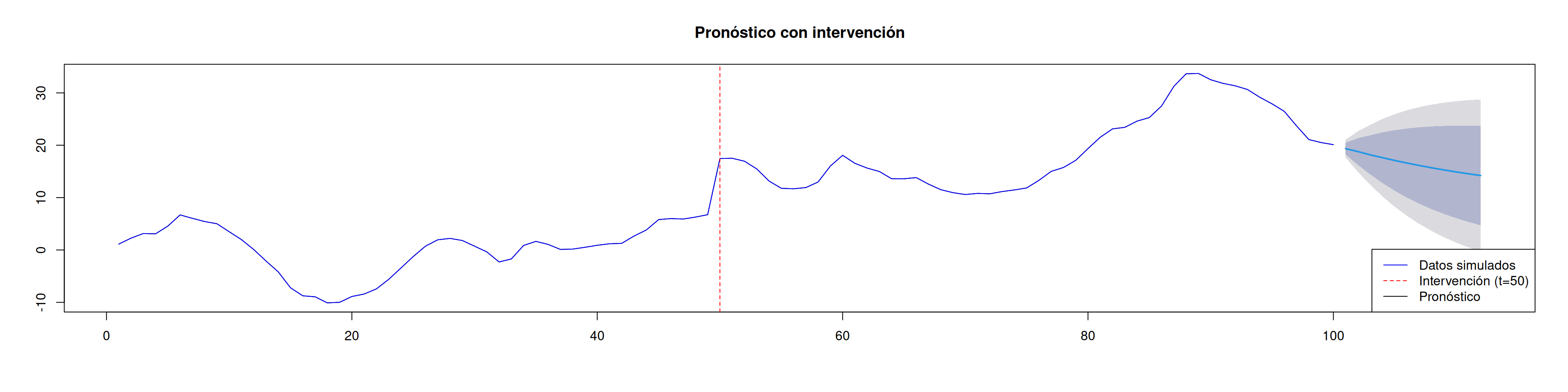
12.6 5. Pronóstico con intervención
Pronosticamos 12 pasos, asumiendo el dummy activo (\(I_t=1\)):
forecast_values <- forecast(model, xreg = rep(1, 12))
#La variable hexogena (outlier) añade 1's en esos 12 adelantos que no tenía registro12.7 6. Visualización de resultados
par(mfrow = c(1,1))
plot(forecast_values, main = "Pronóstico con intervención")
lines(sim_data, col = "blue")
abline(v = 50, col = "red", lty = 2)
legend(
"bottomright",
legend = c("Datos simulados", "Intervención (t=50)", "Pronóstico"),
col = c("blue", "red", "black"),
lty = c(1, 2, 1)
)12.8 Usos y notas prácticas
- Modelos ARIMAX permiten cuantificar el impacto de un choque o política puntual.
- La variable de intervención \(I_t\) puede representar subsidios, promociones, cambios regulatorios, etc.
- Evaluar la significancia del coeficiente \(\beta\) indica si la intervención produjo un cambio duradero en nivel.
- Este enfoque es básico para estudios de evaluación de impacto en series temporales.