phi_inicial <- 0.5
sigma2_inicial <- 1
modAR1 <- dlmModARMA(ar = phi_inicial, ma = NULL, sigma2 = sigma2_inicial)9 MEE - Filtro Kalman
9.1 Descripción del código
En este ejemplo usamos el paquete dlm para ajustar un proceso AR(1) en formato espacio-estado, estimar sus parámetros por Máxima Verosimilitud (MEE) y recuperar los estados no observados mediante el filtro y suavizador de Kalman.
Según las notas de clase, un modelo de espacio-estado se escribe como:
\[
\begin{aligned}
y_t &= Z\,\omega_t + \varepsilon_t, \quad \varepsilon_t \sim N(0,H),\\
\omega_{t+1} &= T\,\omega_t + \eta_t, \quad \eta_t \sim N(0,Q).
\end{aligned}
\] El filtro de Kalman calcula recursivamente el estimador de \(\omega_t\) que minimiza el error cuadrático medio usando solo la información disponible hasta \(t\). El suavizador utiliza toda la muestra hasta \(T\).
9.1.1 1. Instalación y carga del paquete
Uso práctico: dlm facilita la formulación y ajuste de modelos de espacio-estado con ARMA en transición y observación.
9.1.2 2. Definición del modelo AR(1) en espacio-estado
Aquí dlmModARMA construye matrices \(T,\,Z,\,Q,\,H\) internas que representan el AR(1): \[
\omega_{t+1} = \phi\,\omega_t + \eta_t,\quad y_t = \omega_t + \varepsilon_t.
\]
9.1.3 3. Simulación de datos
set.seed(123)
sim_data <- arima.sim(model = list(ar = phi_inicial), n = 100,
sd = sqrt(sigma2_inicial))
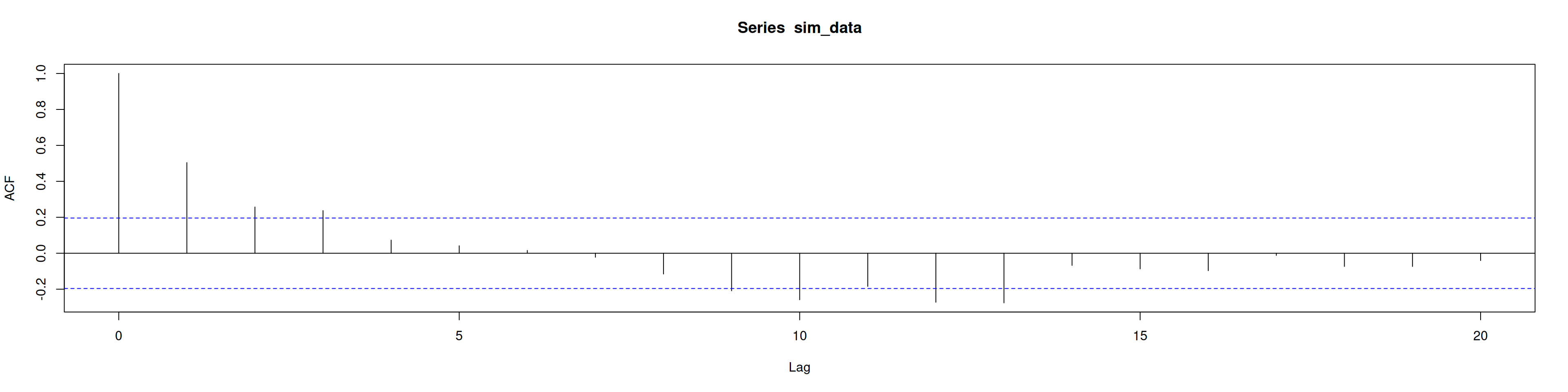
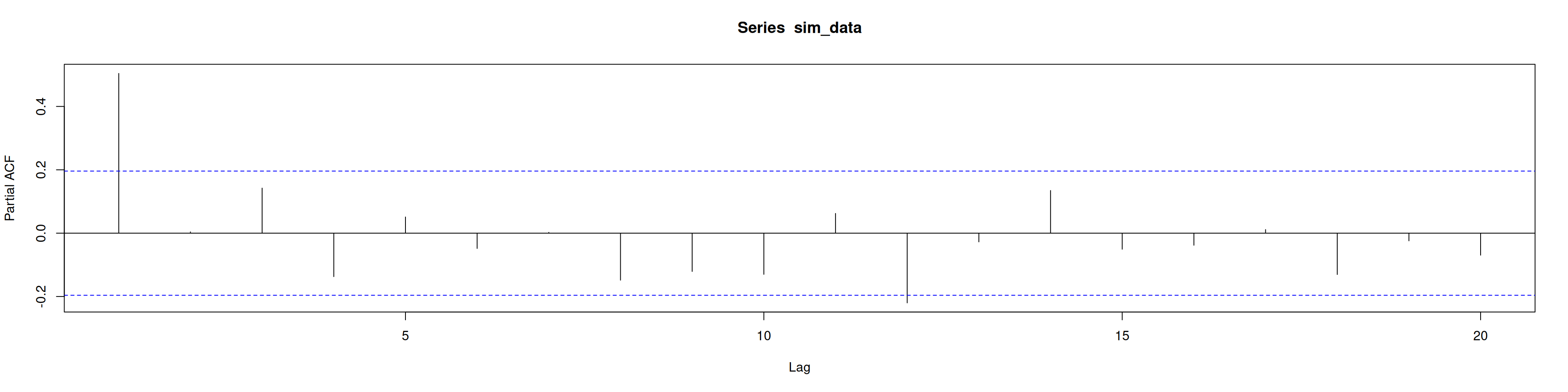
acf(sim_data)pacf(sim_data)La ACF decae exponencialmente, consistente con un AR(1).
9.1.4 4. Función de construcción para MEE
build_mod <- function(par) {
dlmModARMA(ar = par[1], ma = NULL, sigma2 = par[2])
}Esta función será llamada por el optimizador de verosimilitud para proponer nuevos parámetros \(\phi\) y \(\sigma^2\).
9.1.5 5. Estimación por Máxima Verosimilitud (MEE)
fit <- dlmMLE(sim_data, parm = c(phi_inicial, sigma2_inicial),
build = build_mod)dlmMLE maximiza la función de verosimilitud evaluada con el filtro de Kalman.
9.1.6 6. Extracción del modelo ajustado
mod_est <- build_mod(fit$par)
print(mod_est)$FF
[,1]
[1,] 1
$V
[,1]
[1,] 0
$GG
[,1]
[1,] 0.4910977
$W
[,1]
[1,] 0.8043823
$m0
[1] 0
$C0
[,1]
[1,] 1e+07Aquí vemos las matrices ajustadas y las varianzas estimadas.
9.1.7 7. Filtro y suavizador de Kalman
# Filtro recursivo hasta t
filt <- dlmFilter(sim_data, mod_est)
# Suavizador usando toda la muestra
states <- dlmSmooth(filt)filt$mcontiene \(\hat\omega_{t|t-1}\) (estimación “a priori”).
states$scontiene \(\hat\omega_{t|T}\) (suavizado “a posteriori”).
9.1.8 8. Visualización de estados
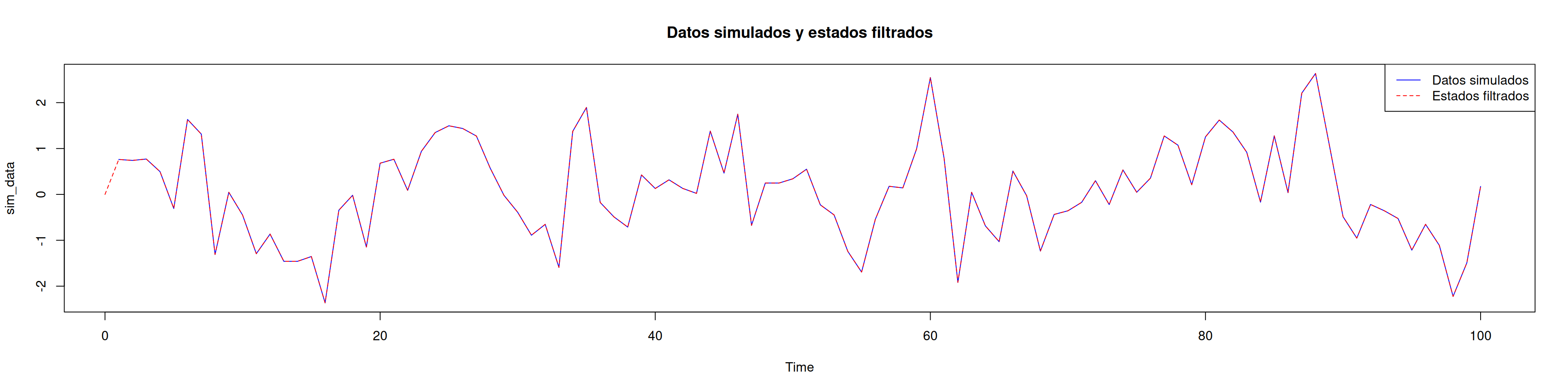
# Estados filtrados en línea continua
plot(sim_data, type="l", col="blue",
main="Datos simulados y estados filtrados")
lines(filt$m, col="red", lty=2)
legend("topright",
legend=c("Datos simulados","Estados filtrados"),
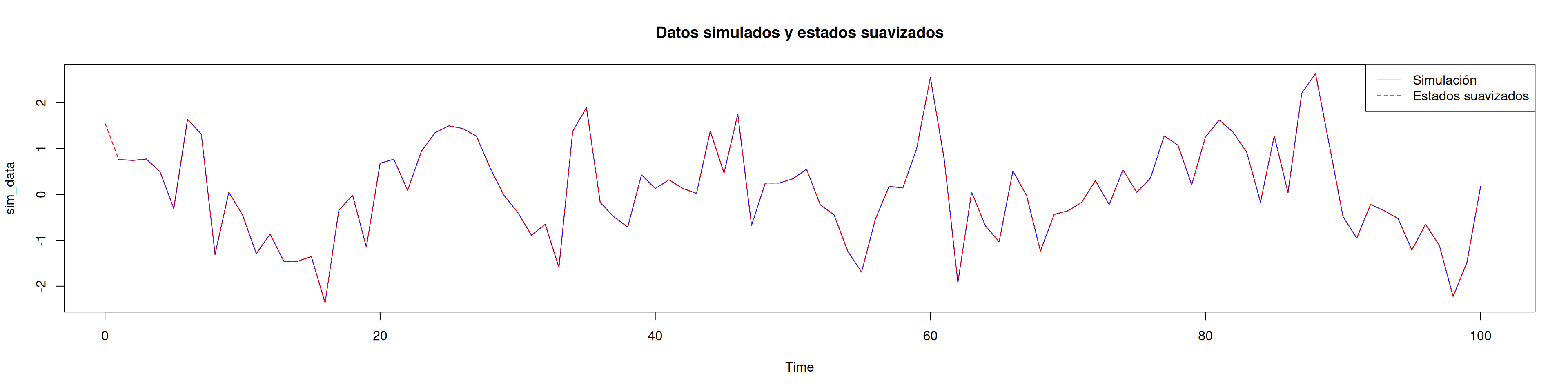
col=c("blue","red"), lty=1:2)# Estados suavizados en línea punteada
plot(sim_data, type="l", col="blue",
main="Datos simulados y estados suavizados")
lines(states$s, col="red", lty=2)
legend("topright",
legend=c("Simulación","Estados suavizados"),
col=c("blue","red"), lty=1:2)9.2 Interpretaciones y usos
- Máxima Verosimilitud (MEE): el filtro de Kalman calcula la verosimilitud del espacio-estado, permitiendo estimar \(\phi\) y \(\sigma^2\) eficientemente.
- Filtro de Kalman: recupera la trayectoria latente \(\omega_t\), útil para detectar cambios en la dinámica subyacente (e.g., en volatilidad o tendencia).
- Suavizado: produce estimaciones más estables de \(\omega_t\) usando toda la información, ideal para análisis retrospectivo de anomalías.
- Extensión: la misma estructura admite modelos ARMA(p,q), componentes estacionales SARIMA en transición, y variables exógenas agregando estados.
Estas herramientas son fundamentales en series de tiempo estructurales y pronósticos en contextos económicos, financieros o de control.