rm(list=ls(all=TRUE))
library(urca); library(forecast); library(tseries)
library(lmtest); library(uroot); library(fUnitRoots)
library(sarima); library(aTSA); require("PolynomF")10 SARIMA(p,d,q)(P,D,Q)_[s]
10.1 Ejercicio de Simulación SARIMA
En esta práctica simulamos distintos procesos estacionales para identificar componentes SARIMA.
Recordemos el operador de diferencia estacional de periodo (s): \[
\Delta_s = 1 - B^s, \text{y el modelo multiplicativo} \\
SARIMA((p,d,q),(P,D,Q)[s]): \\ \Phi(B^s),\phi(B),(1 - B)^d,(1 -
B^s)^D X_t ;=;\Theta(B^s),\theta(B),w_t. \]
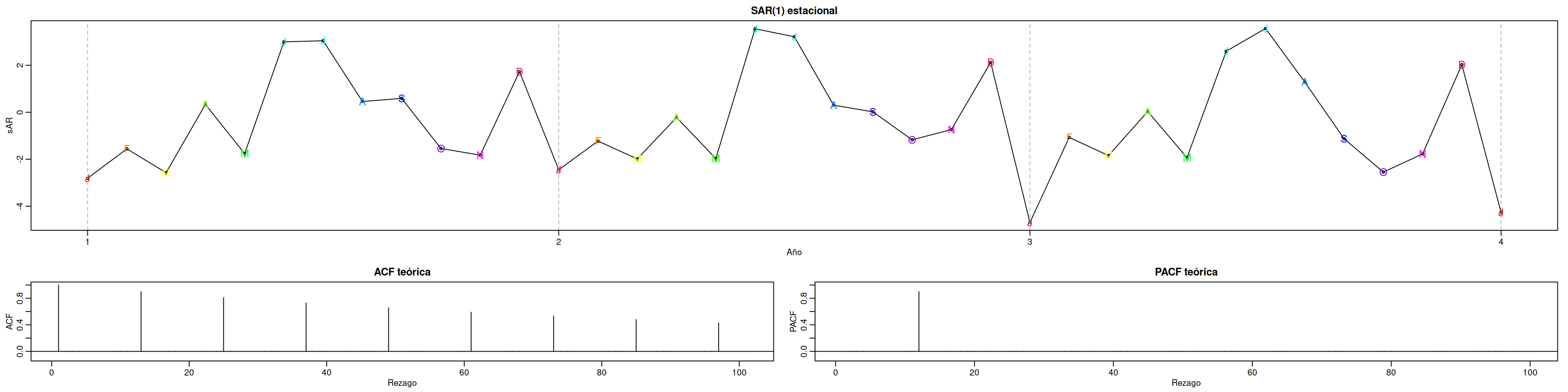
10.2 1. SAR(1) estacional ((0,0,0)(1,0,0)[12])
Simulamos \[X_t = \Phi*1,X*{t-12} + w_t,\quad \Phi\_1=0.9,\] y comparamos su ACF/PACF teórica y muestral.
set.seed(666)
phi <- c(rep(0,11), .9)
sAR <- ts(arima.sim(list(order=c(12,0,0), ar=phi), n=37), frequency=12)
layout(matrix(c(1,1,2,1,1,3), nc=2))
par(mar=c(3,3,2,1), mgp=c(1.6,.6,0))
# Serie con marcadores para cada mes
plot(sAR, axes=FALSE, main="SAR(1) estacional", xlab="Año", type="o")
months <- c("J","F","M","A","M","J","J","A","S","O","N","D")
points(sAR, pch=months, col=rainbow(12), cex=1.2)
axis(1, 1:4); abline(v=1:4, lty=2, col=gray(.7)); axis(2); box()
# ACF y PACF teórica
ACF <- ARMAacf(ar=phi, ma=0, 100)
PACF <- ARMAacf(ar=phi, ma=0, 100, pacf=TRUE)
plot(ACF, type="h", xlab="Rezago", main="ACF teórica", ylim=c(-.1,1)); abline(h=0)
plot(PACF, type="h", xlab="Rezago", main="PACF teórica", ylim=c(-.1,1)); abline(h=0)Interpretación:
- La ACF exhibe picos cada 12 lags, característica de estacionalidad de periodo (s=12).
- La PACF muestra un solo pico en rezago 12, indicando un término SAR(1).
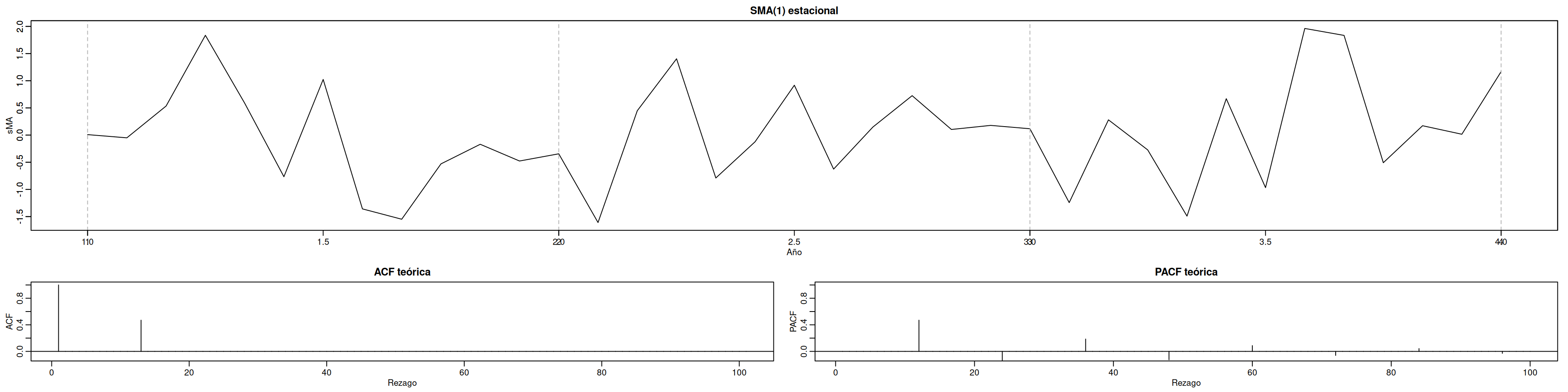
10.3 2. SMA(1) estacional ((0,0,0)(0,0,1)[12])
Simulamos $$X_t = w_t + *1,w*{t-12},_1=0.7.$$
set.seed(123)
theta <- c(rep(0,11), .7)
sMA <- ts(arima.sim(list(order=c(0,0,12), ma=theta), n=37), frequency=12)
layout(matrix(c(1,1,2,1,1,3), nc=2))
par(mar=c(3,3,2,1), mgp=c(1.6,.6,0))
plot(sMA, main="SMA(1) estacional", xlab="Año", type="l")
axis(1,1:4); abline(v=1:4,lty=2,col=gray(.7)); axis(2); box()
ACF <- ARMAacf(ma=theta, ar=0, 100)
PACF <- ARMAacf(ma=theta, ar=0, 100, pacf=TRUE)
plot(ACF, type="h", xlab="Rezago", main="ACF teórica", ylim=c(-.1,1)); abline(h=0)
plot(PACF, type="h", xlab="Rezago", main="PACF teórica", ylim=c(-.1,1)); abline(h=0)Uso práctico:
- Un pico en ACF en rezago 12 y decaimiento rápido en PACF sugiere término SMA(1).
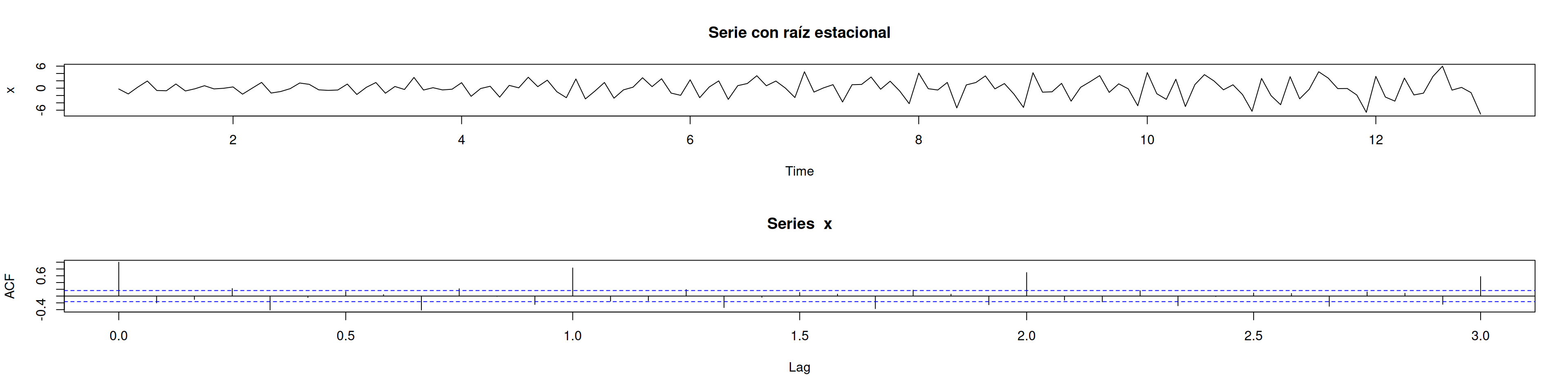
10.4 3. Raíz unitaria estacional
Simulamos un proceso con una raíz estacional unitaria ((D=1)) y verificamos diferencias:
set.seed(123)
x <- ts(sim_sarima(n=144,
model=list(iorder=0, siorder=1, nseasons=12, sigma2=1),
n.start=24), frequency=12)
par(mfrow=c(2,1))
plot(x, main="Serie con raíz estacional")
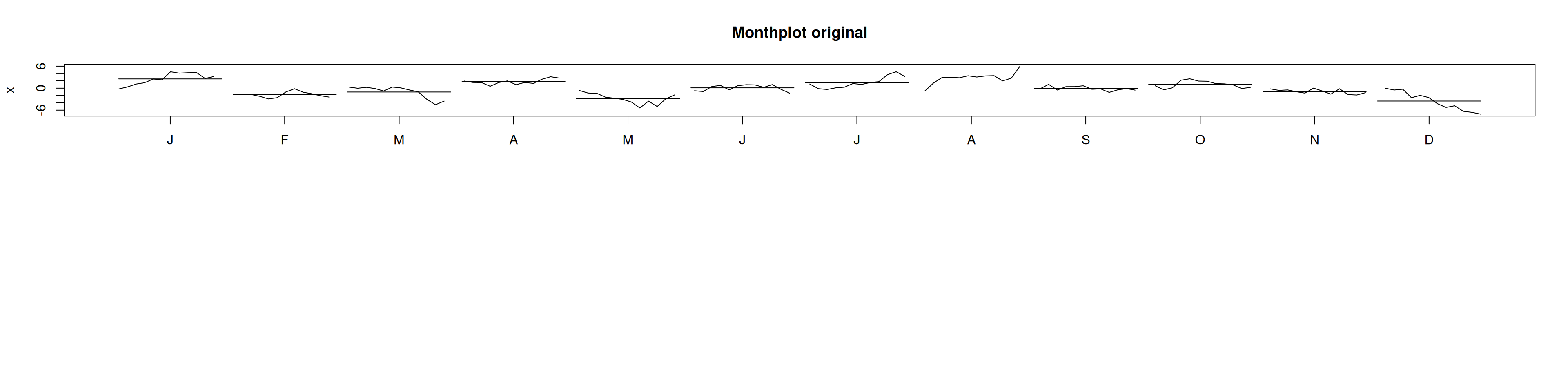
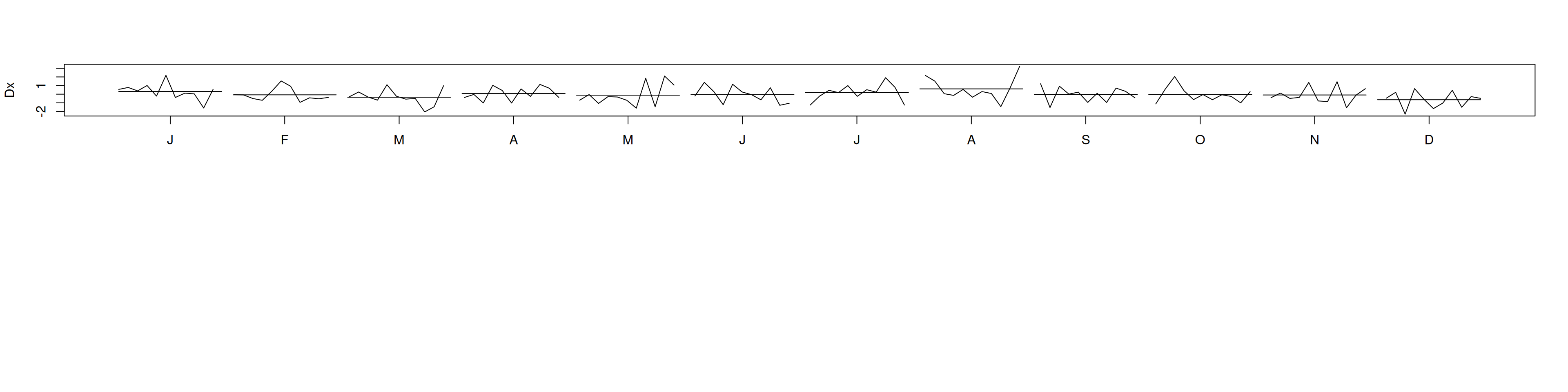
acf(x, lag.max=36)monthplot(x, main="Monthplot original")
# Número de diferencias estacionales necesarias
nsdiffs(x)[1] 1Dx <- diff(x, lag=12)
par(mfrow=c(2,1))
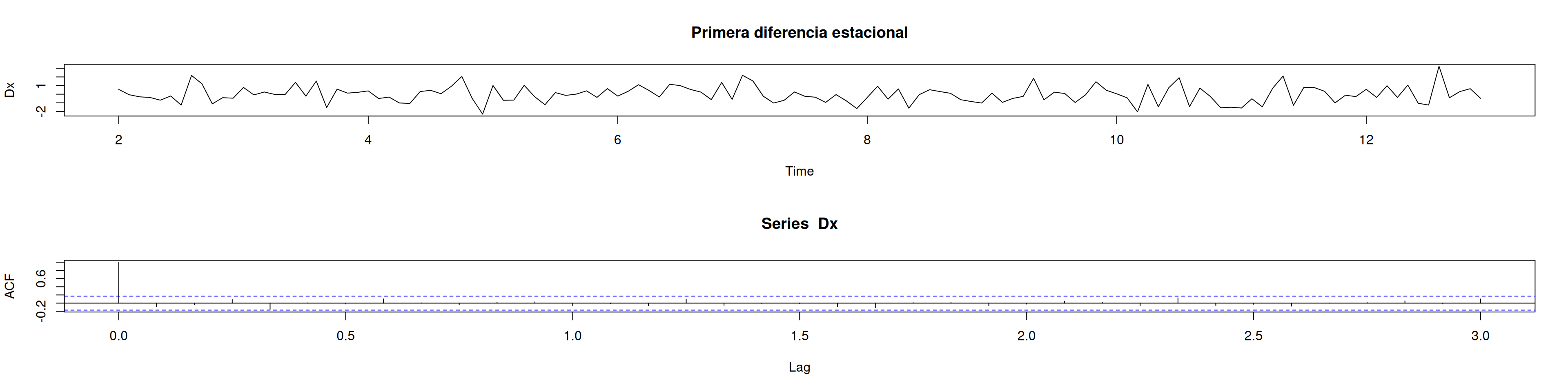
plot(Dx, main="Primera diferencia estacional")
acf(Dx, lag.max=36)monthplot(Dx)
nsdiffs(Dx)[1] 0Interpretación:
- nsdiffs(x) recomienda (D=1).
- Tras diferenciar estacionalmente, la ACF pierde picos periódicos, serie aparenta estacionaria.
10.5 4. SAR(1) estacional con simulación extendida
Simulación con coeficiente 0.8 en rezago 12:
set.seed(123)
x1 <- ts(sim_sarima(n=144,
model=list(ar=c(rep(0,11),0.8)),
n.start=24), frequency=12)
layout(matrix(c(1,1,2,1,1,3), nc=2))
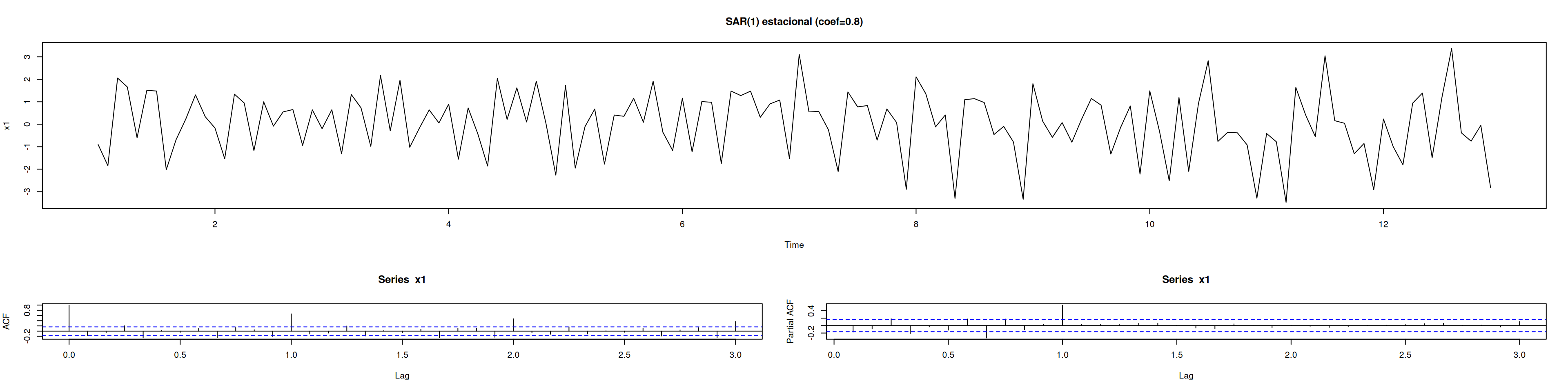
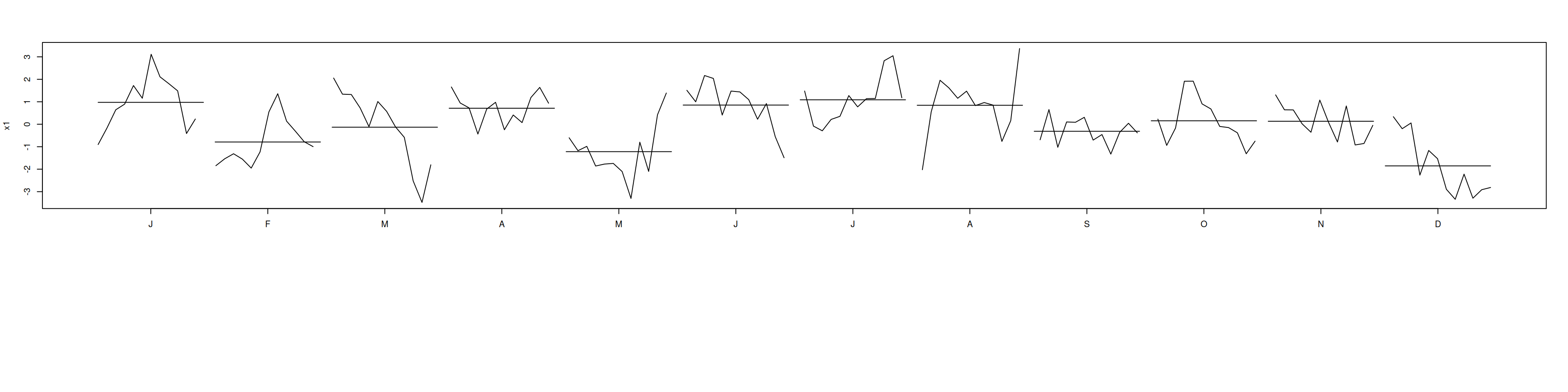
plot(x1, main="SAR(1) estacional (coef=0.8)")
acf(x1, lag.max=36); pacf(x1, lag.max=36)monthplot(x1); nsdiffs(x1); ndiffs(x1)[1] 1[1] 0# Comprobar cercanía a raíz unitaria
p <- polynom(c(1, rep(0,11), -0.8))
roots <- solve(p)
abs(roots) [1] 1.018769 1.018769 1.018769 1.018769 1.018769 1.018769 1.018769 1.018769
[9] 1.018769 1.018769 1.018769 1.018769Nota: raíces cercanas al círculo unitario indican comportamiento casi integrado estacional.
10.6 5. SARIMA(0,0,1)(1,1,0)[12] y SARIMA(0,0,1)(0,1,1)[12]
set.seed(2025)
x3 <- ts(sim_sarima(n=144,
model=list(sar=0.8, ma=-0.5, iorder=0, siorder=1, nseasons=12),
n.start=24), frequency=12)
layout(matrix(c(1,1,2,1,1,3), nc=2))
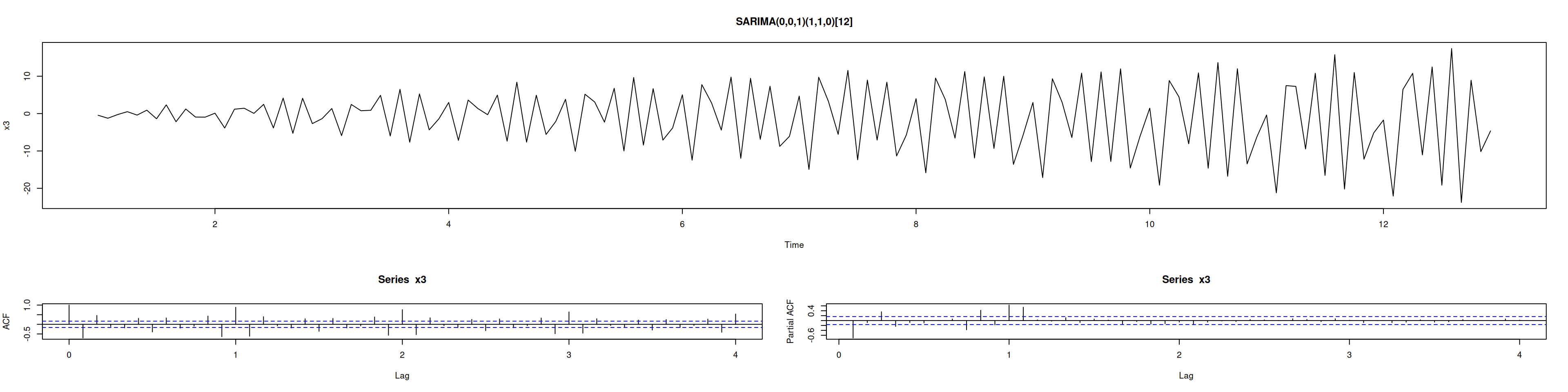
plot(x3, main="SARIMA(0,0,1)(1,1,0)[12]")
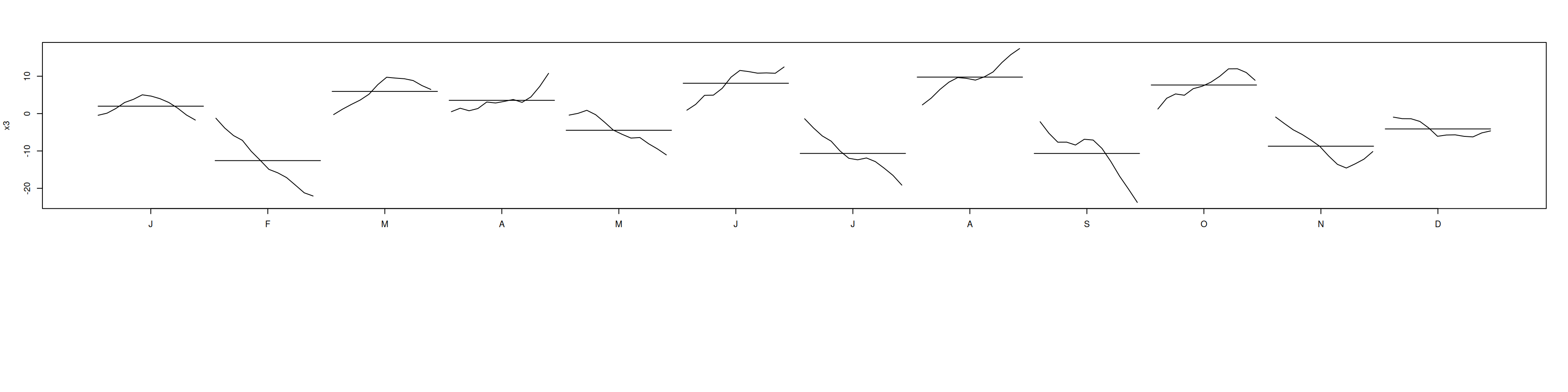
acf(x3, lag.max=48); pacf(x3, lag.max=48)monthplot(x3); nsdiffs(x3)[1] 1# Diferencia estacional
Dx3 <- diff(x3, lag=12)
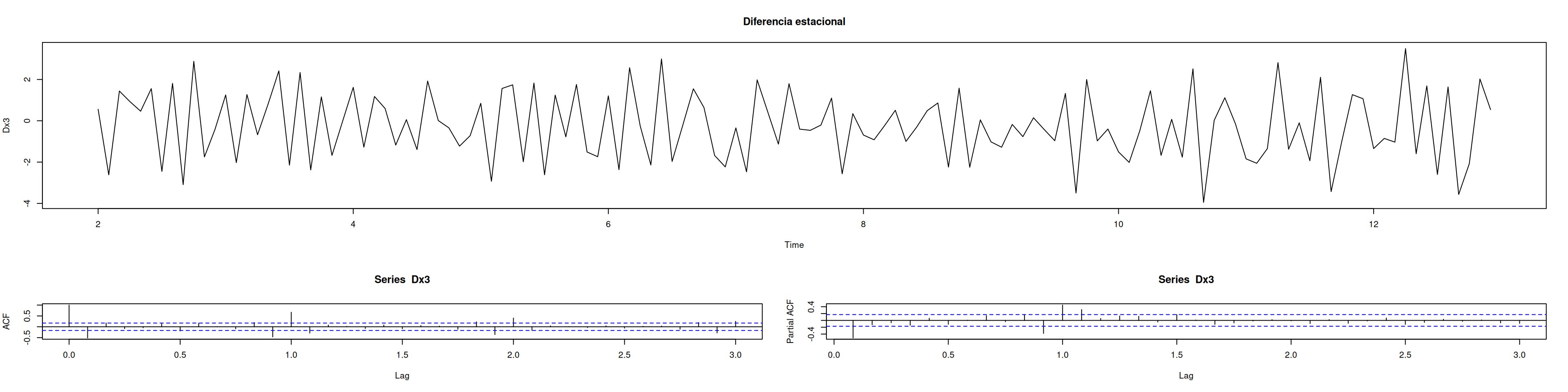
layout(matrix(c(1,1,2,1,1,3), nc=2))plot(Dx3, main="Diferencia estacional")
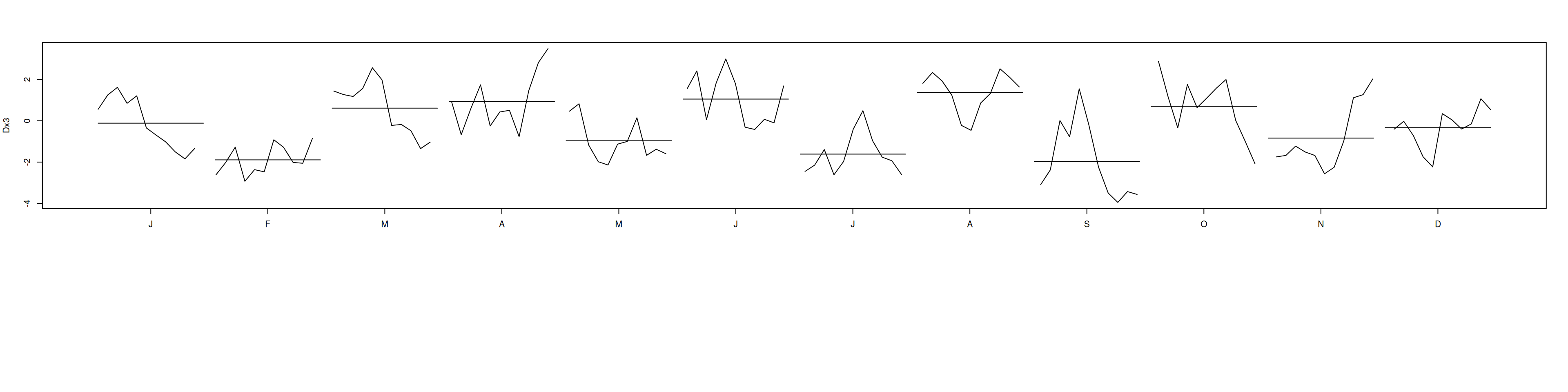
acf(Dx3, lag.max=36); pacf(Dx3, lag.max=36); monthplot(Dx3); nsdiffs(Dx3)[1] 1# Comparación de modelos en original vs diferenciado
auto.arima(x3)Series: x3
ARIMA(0,0,1)(1,1,0)[12] with drift
Coefficients:
ma1 sar1 drift
-0.4909 0.7578 -0.0186
s.e. 0.0863 0.0568 0.0118
sigma^2 = 0.9426: log likelihood = -187.14
AIC=382.28 AICc=382.6 BIC=393.81auto.arima(Dx3)Series: Dx3
ARIMA(0,0,1)(0,1,0)[12]
Coefficients:
ma1
-0.4545
s.e. 0.0983
sigma^2 = 1.039: log likelihood = -172.18
AIC=348.35 AICc=348.45 BIC=353.93set.seed(2025)
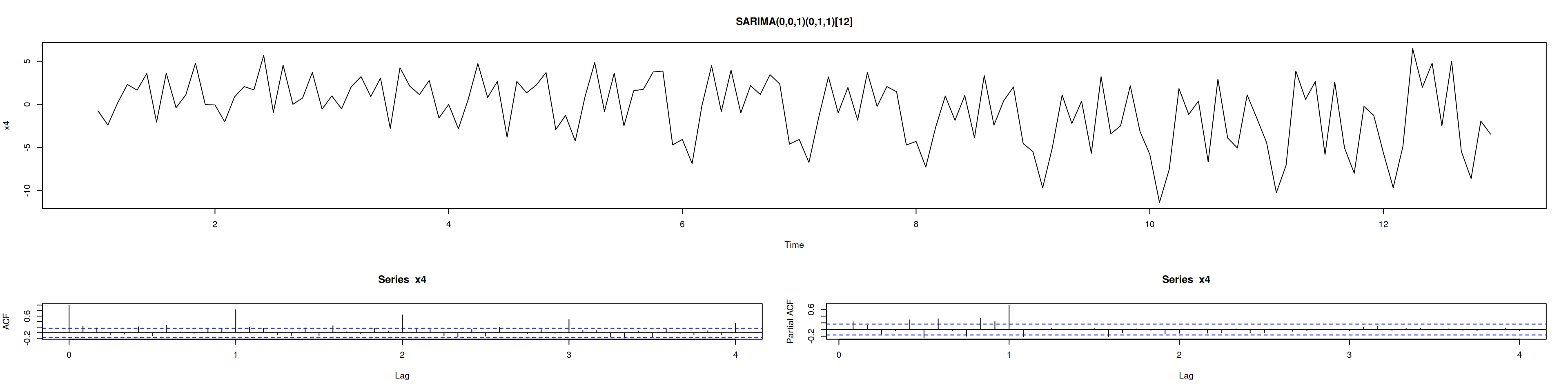
x4 <- ts(sim_sarima(n=144,
model=list(ma=0.6, sma=0.5, iorder=0, siorder=1, nseasons=12),
n.start=36), frequency=12)
layout(matrix(c(1,1,2,1,1,3), nc=2))
plot(x4, main="SARIMA(0,0,1)(0,1,1)[12]")
acf(x4, lag.max=48); pacf(x4, lag.max=48)# Diferencia estacional
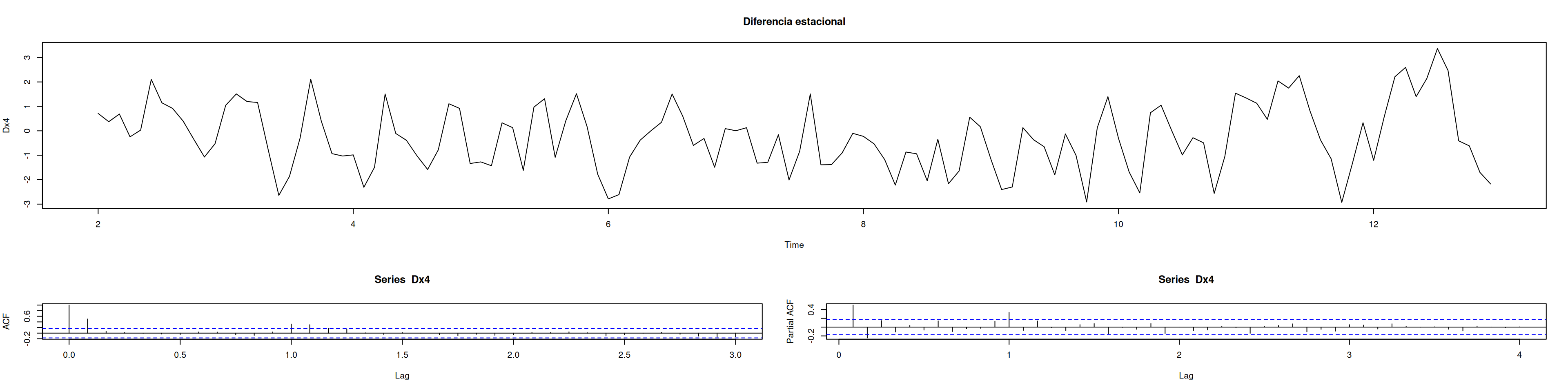
Dx4 <- diff(x4, lag=12)
plot(Dx4, main="Diferencia estacional")
acf(Dx4, lag.max=36); pacf(Dx4, lag.max=48); nsdiffs(Dx4)[1] 0# Modelos sugeridos
auto.arima(x4)Series: x4
ARIMA(0,0,1)(0,1,1)[12]
Coefficients:
ma1 sma1
0.6724 0.4596
s.e. 0.0633 0.0831
sigma^2 = 1.031: log likelihood = -190.01
AIC=386.02 AICc=386.21 BIC=394.67auto.arima(Dx4)Series: Dx4
ARIMA(0,0,1)(0,0,1)[12] with zero mean
Coefficients:
ma1 sma1
0.6724 0.4596
s.e. 0.0633 0.0831
sigma^2 = 1.031: log likelihood = -190.01
AIC=386.02 AICc=386.21 BIC=394.6710.6.1 Notas de uso y modelado
- Identificación:
- ACF estacional: picos en múltiplos de (s=12).
- PACF estacional: corte después de (P) en rezago 12.
- ACF estacional: picos en múltiplos de (s=12).
- Diferenciación:
- Use
nsdiffspara decidir el número de diferencias estacionales (D).
- Use
ndiffspara diferencias regulares (d).
- Use
- Selección de modelo:
- Combine patrones ACF/PACF con criterios AIC/BIC.
- Estime con
auto.arima(..., seasonal=TRUE)osarima.
- Combine patrones ACF/PACF con criterios AIC/BIC.
- Diagnóstico:
- Verifique residuos (ACF, Ljung–Box).
- Compruebe estacionariedad tras diferencias regulares y estacionales.
- Verifique residuos (ACF, Ljung–Box).
- Pronóstico:
- Una vez identificado y diagnosticado, use el modelo para pronósticos con
forecast.
- Una vez identificado y diagnosticado, use el modelo para pronósticos con
Este flujo corresponde al método Box–Jenkins extendido a modelos estacionales SARIMA.