5  ACF en AR(p) y MA(q)

5.1 Simulación y cálculo de ACF para n = 500 y n = 50

# Serie MA(3) con n = 500
set.seed(1)
x1 <- filter(rnorm(500 + 2), filter = rep(1/3, 3), sides = 2)
x1 <- x1[2:(500 + 1)]

# Serie MA(3) con n = 50
x2 <- filter(rnorm(50 + 2), filter = rep(1/3, 3), sides = 2)
x2 <- x2[2:(50 + 1)]

par(mfrow = c(1,2))
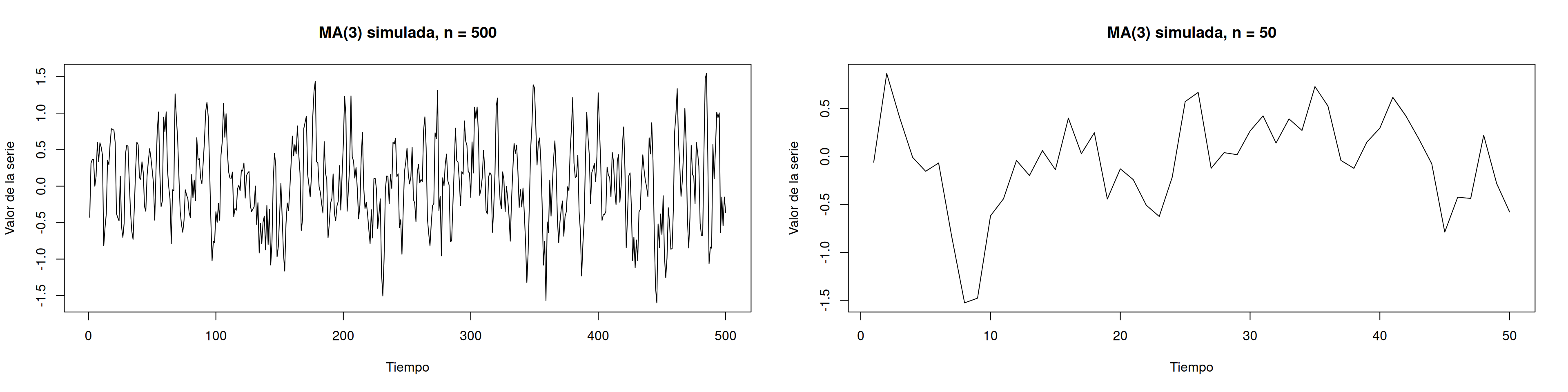
plot.ts(x1, main = "MA(3) simulada, n = 500", xlab = "Tiempo", ylab = "Valor de la serie")
plot.ts(x2, main = "MA(3) simulada, n = 50", xlab = "Tiempo", ylab = "Valor de la serie")

5.2 Función teórica de la ACF para MA(3)

\[ \rho(h) = \begin{cases} 1, & h = 0,\\[6pt] \frac{2}{3}, & |h| = 1,\\[6pt] \frac{1}{3}, & |h| = 2,\\[6pt] 0, & |h| > 2. \end{cases} \]

5.3 Cálculo y comparación de ACFs muestrales

# ACF muestral comparativa
par(mfrow = c(1,2))
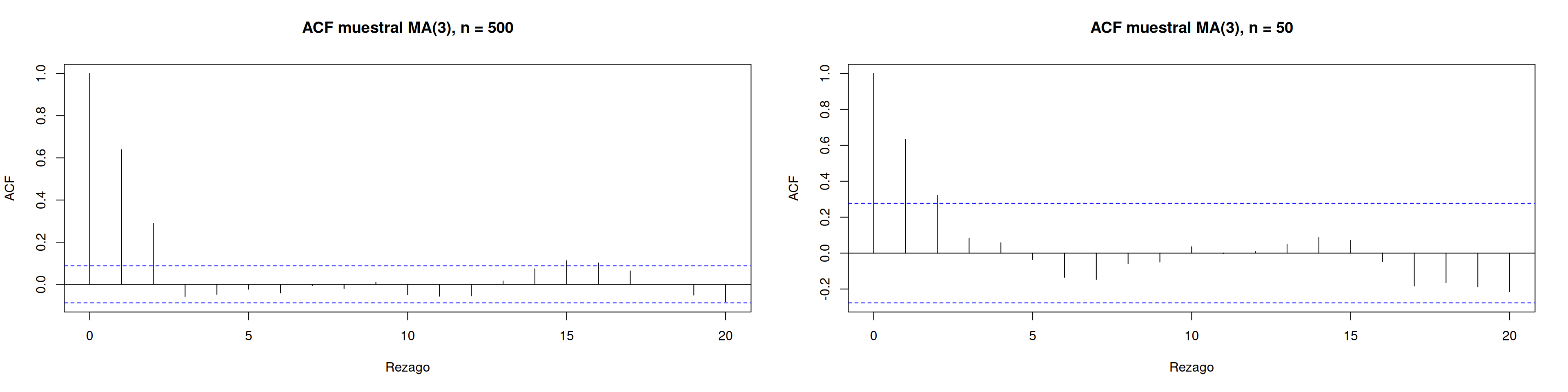
acf(x1, lag.max = 20, main = "ACF muestral MA(3), n = 500", xlab = "Rezago", ylab = "ACF")
acf(x2, lag.max = 20, main = "ACF muestral MA(3), n = 50", xlab = "Rezago", ylab = "ACF")

acf_x1 <- acf(x1, lag.max = 20, plot = FALSE)$acf
acf_x2 <- acf(x2, lag.max = 20, plot = FALSE)$acf
rho_teo <- c(1, 2/3, 1/3, rep(0, 18))

# Construir tabla comparativa
Autocorrelaciones <- data.frame(
  Rezago            = 0:20,
  ACF500_Estimada   = round(acf_x1,   4),
  ACF50_Estimada    = round(acf_x2,   4),
  ACF_Teórica       = round(rho_teo,  4)
)
head(Autocorrelaciones, 6)

  Rezago ACF500_Estimada ACF50_Estimada ACF_Teórica
1      0          1.0000         1.0000      1.0000
2      1          0.6390         0.6337      0.6667
3      2          0.2893         0.3215      0.3333
4      3         -0.0575         0.0830      0.0000
5      4         -0.0477         0.0580      0.0000
6      5         -0.0234        -0.0354      0.0000

5.4 Interpretación de resultados

Para rezagos (h=0, , ), los valores muestrales de ambas series (n=500 y n=50) están muy cercanos a los valores teóricos ((1, 2/3, 1/3)). Sin embargo, al observar los autocorrelogramas se observa lo siguiente:

• Muestra grande (n = 500): las bandas de confianza son más estrechas y la variabilidad de los coeficientes para (|h|>2) es menor, manteniéndose cerca de cero.
  
• Muestra pequeña (n = 50): las bandas de confianza se amplían y los coeficientes de autocorrelación muestran mayor dispersión, por lo que para (|h|>2) aparecen valores más alejados de cero.

Este comportamiento refleja que con mayor tamaño de muestra la estimación de la ACF es más estable y confiable, especialmente para rezagos fuera del orden del modelo MA(3).